Advertisements
Advertisements
Question
Line ℓ touches a circle with center O at point P. If the radius of the circle is 9 cm, answer the following.
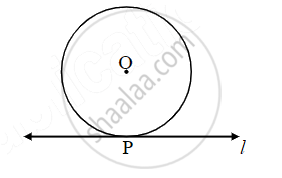
If d(O, Q) = 8 cm, where does the point Q lie?
Solution
Here, 8 cm < 9 cm
∴ d(O, Q) < d(O, P)
∴ d(O, Q) < radius
∴ Point Q lies in the interior of the circle.
APPEARS IN
RELATED QUESTIONS
If two circles with radii 5 cm and 3 cm respectively touch internally, find the distance between their centres.
If two circles with radii 8 cm and 3 cm, respectively, touch internally, then find the distance between their centers.
If two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres.
Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres
In the given figure, the circles with centres P and Q touch each other at R. A line passing through R meets the circles at A and B respectively. Prove that – (1) seg AP || seg BQ,
(2) ∆APR ~ ∆RQB, and
(3) Find ∠ RQB if ∠ PAR = 35°
In the given figure, ray PQ touches the circle at point Q. PQ = 12, PR = 8, find PS and RS.
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other. What is the distance between their centers ?
Four alternative answers for the following question is given. Choose the correct alternative.
A circle touches all sides of a parallelogram. So the parallelogram must be a, ______
Line l touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.
- What is d(O, P) = ? Why?
- If d(O, Q) = 8 cm, where does the point Q lie?
- If d(O, Q) = 15 cm, How many locations of point Q are line on line l? At what distance will each of them be from point P?

In the adjoining figure circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill in the blanks and complete the proof.
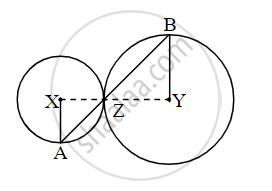
Construction: Draw segments XZ and YZ.
Proof:
By theorem of touching circles, points X, Z, Y are `square`.
∴ ∠XZA ≅ `square` ...(opposite angles)
Let ∠XZA = ∠BZY = a ...(I)
Now, seg XA ≅ seg XZ ...[Radii of the same circle]
∴∠XAZ = `square` = a ...[isosceles triangle theorem](II)
Similarly,
seg YB ≅ seg YZ ...[Radii of the same circle]
∴∠BZY = `square` = a ...[isosceles triangle theorem](III)
∴ from (I), (II), (III),
∠XAZ = `square`
∴ radius XA || radius YZ ...[`square`]
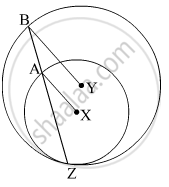
In the given figure, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger circle and it itersects smaller circle at point A. Prove that, seg AX || seg BY.
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other externally. What is the distance between their centres?
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles having diameters 8 cm and 6 cm touch each other internally. Find the distance between their centres.
Line ℓ touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.

If d(O, R) = 15 cm, how many locations of point R are line on line l? At what distance will each of them be from point P?
A circle with centre P is inscribed in the ∆ABC. Side AB, side BC, and side AC touch the circle at points L, M, and N respectively. The radius of the circle is r.
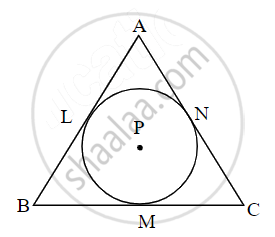
Prove that: A(ΔABC) = `1/2` (AB + BC + AC) × r
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
