Advertisements
Advertisements
Question
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
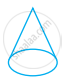
Solution
In the given figure, we have
Faces (F) = 2, Vertices (V) = 1 and Edges (E) = 0
On putting these values in Euler's formula, we get
F + V – E = 2
⇒ 2 + 1 – 0 = 2
⇒ 3 ≠ 2
Hence, these values do not satisfy the Euler's formula. So, it is not a polyhedra.
APPEARS IN
RELATED QUESTIONS
Verify Euler’s formula for the following three-dimensional figures:

In a solid if F = V = 5, then the number of edges in this shape is ______.
If the sum of number of vertices and faces in a polyhedron is 14, then the number of edges in that shape is ______.
Complete the table given below:
| S.No | Solid | Shape of Solid |
Number of faces F |
Number of Verticles V |
Number of edges E |
F + V | E + 2 |
| a. | Cuboid |  |
|||||
| b. | Triangular Pyramid |
 |
|||||
| c. | Square Pyramid |
 |
|||||
| d. | Rectangular Pyramid |
 |
|||||
| e. | Pentagonal Pyramid |
 |
|||||
| f. | Hexagonal Pyramid |
 |
|||||
| g. | Triangular Prism |
 |
|||||
| h. | Square Prism |
 |
|||||
| i. | Cube |  |
|||||
| j. | Pentagonal Prism |
 |
|||||
| k. | Octagonal Prism |
 |
|||||
| l. | Heptagonal Prism |
 |
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.

Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
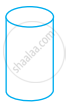
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
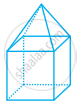
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
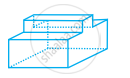
Using Euler’s formula, find the value of unknown z in the following table.
| Faces | 9 |
| Vertices | z |
| Edges | 16 |
A polyhedron has 20 faces and 12 vertices. Find the edges of the polyhedron.
