Question

मान लीजिए A और B सामान त्रिज्याओ वाले दो वृतो के केंद्र है। इन्हें इस परकार खींचिए ताकि एक वृत्त दूसरे के केंद्र से होकर जाए। इन्हें C और D पर प्रतिछेदित करने दीजिए।जाँच कीजिए कि `overline("AB")` और `overline"CD"` परस्पर समकोण पर है। 

Answer 1

आइए एक ही त्रिज्या के दो वृत्त बनाएं जो दूसरे वृत्त के केंद्रों से होकर गुजर रहे हों।

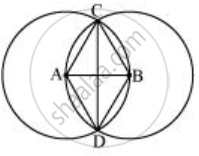
यहाँ, बिंदु A और B इन वृत्तों के केंद्र हैं और ये वृत्त एक दूसरे को बिंदु C और D पर प्रतिच्छेद कर रहे हैं।

चतुर्भुज ADBC में,

AD = AC (ए पर केन्द्रित वृत्त की त्रिज्या)

BC = BD (B पर केन्द्रित वृत्त की त्रिज्या)

चूँकि दोनों वृत्तों की त्रिज्याएँ समान हैं, इसलिए, AD = AC = BC = BD

अतः `square`ADBC एक समचतुर्भुज है और एक समचतुर्भुज में, विकर्ण एक दूसरे को 90° पर समद्विभाजित करते हैं। अतः AB और CD समकोण पर हैं।