Advertisements
Advertisements
प्रश्न
मान लीजिए A और B सामान त्रिज्याओ वाले दो वृतो के केंद्र है। इन्हें इस परकार खींचिए ताकि एक वृत्त दूसरे के केंद्र से होकर जाए। इन्हें C और D पर प्रतिछेदित करने दीजिए।जाँच कीजिए कि `overline("AB")` और `overline"CD"` परस्पर समकोण पर है।
उत्तर
आइए एक ही त्रिज्या के दो वृत्त बनाएं जो दूसरे वृत्त के केंद्रों से होकर गुजर रहे हों।
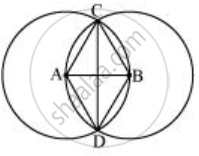
यहाँ, बिंदु A और B इन वृत्तों के केंद्र हैं और ये वृत्त एक दूसरे को बिंदु C और D पर प्रतिच्छेद कर रहे हैं।
चतुर्भुज ADBC में,
AD = AC (ए पर केन्द्रित वृत्त की त्रिज्या)
BC = BD (B पर केन्द्रित वृत्त की त्रिज्या)
चूँकि दोनों वृत्तों की त्रिज्याएँ समान हैं, इसलिए, AD = AC = BC = BD
अतः `square`ADBC एक समचतुर्भुज है और एक समचतुर्भुज में, विकर्ण एक दूसरे को 90° पर समद्विभाजित करते हैं। अतः AB और CD समकोण पर हैं।
APPEARS IN
संबंधित प्रश्न
एक ही केंद्र O लेकर 4 सेमी और 2.5 सेमी त्रिज्या वाले दो वृत्त खींचिए।
एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को जोड़ दें, तो कौन सी आकृति प्राप्त होती है? यदि व्यास परस्पर लंब हों, तो कौन सी आकृति प्राप्त होगी? आप अपने उत्तर की जाँच किस प्रकार करेंगे?
एक वृत्त खींचिए और बिंदु A, B और C इस प्रकार अंकित कीजिए कि
- A वृत्त पर स्थित हो।
- B वृत्त के अभ्यंतर में स्थित हो।
- C वृत्त के बहीर्भाग में स्थित हो।
