Question

एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को जोड़ दें, तो कौन सी आकृति प्राप्त होती है? यदि व्यास परस्पर लंब हों, तो कौन सी आकृति प्राप्त होगी? आप अपने उत्तर की जाँच किस प्रकार करेंगे?

Answer 1

विवरण - O केंद्र से एक वृत्त खींचकर उसमें दो व्यास बनाए जिन्हें नाम दिया AB और CD। यदि इन व्यासों के सिरों को मिला दिया जाए, तो एक आकृति बनेगी जो एकआयात होगी, इस बात को हम निम्नलिखित रूप में सिद्ध करेंगे। 

O केंद्र है तथा व्यास AB तथा CD को प्रतिछेदित बिन्दु भी है। 

इसलिए 

OC = OD तथा OA = OB

(एक ही वृत्त की सामान त्रिज्याए) 

CB = AD तथा AC = DB

केंद्र के सम दुरी पर स्थित जिवाएं सामान होती है। 

∠A = ∠B = ∠C = ∠D = 90°

(∆ACB तथा ∆ADB है।) 

(∆CBD तथा ∆CAD सर्वांगसम है।) 

 इसलिए ∠A, ∠B, ∠C, ∠D सर्वांगसम है। 

चतुर्भुज के चारो कोण सामान हो तो एक कोण का माप 90° होता है। 

इसलिए यह एक आयत है। (सम्मुख भुजाएं सामान होती है तथा प्रत्येक कोण 90° का है।)

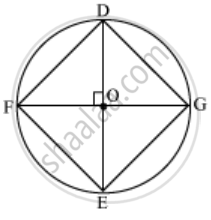
यदि व्यास परस्पर लंब हो तो सिरों को मिलने से प्राप्त आकृति एक वर्ग होगी। जांच के लिए हम विवरण इस प्रकार देंगे। 

DE तथा FG व्यास परस्पर लंब है, तो 

∠FOD, ∠GOD, ∠FOE, ∠GOE = 90°

व्यास के सिरों को मिलने से को त्रिभुज बनेंगे वे समबाहु त्रिभुज होंगे इसलिए उनसे बना चतुर्भुज होगा अर्थात एक वर्ग होगा।