Advertisements
Advertisements
Question
Minimize : Z = 3x1 + 2x2
Subject to constraints
5x1 + x2 ≥ 10
2x1 + 2x2 ≥ 12
x1 + 4x2 ≥ 12
x1 , x2 ≥ 0
Solution
| In equation | Equation | Points | Region |
| 5x1 + x2 ≥ 10 | 5x1 + x2 = 10 | A (2,0) , B (0 , 10) |
Non-origin |
| 2x1 + 2x2 ≥ 12 | 2x1 + 2x2 = 12 | C (6 , 0) , D (0 , 6) |
Non-origin |
| x1 + 4x2 ≥ 12 | x1 + 4x2 = 12 | E (12 , 0) , F (0 , 3) |
Non-origin |
| x1 , x2 ≥ 0 | I st quadrant | ||
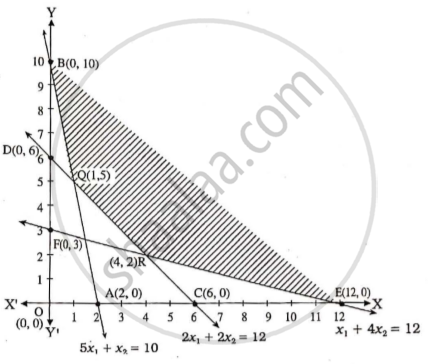
BQRE - unbounded feasible region
At B (O, 10), Z = 3 (0) + 2 (10) = 20
Q (l, 5 }, z = 3 (1) + 2 (5) = 13
R (4, 2), Z = 3 _(4) + 2 (2) = 16
E (12, 0), Z = 3 (12) + 2 (0) = 36
Z is minimum at Q (1 , 5) and the minimum value is Z = 13.
APPEARS IN
RELATED QUESTIONS
Electro Corp. Co. manufactures two electrical products :Air conditioners and Fans. The assembly process for each is similar in which both require a certain amount of wiring and drilling. Each air conditioner takes 4 hours for wiring and 2 hours for drilling. Each fan also takes 2 hours for wiring and 1 hour for drilling. During the next production period, 240 hours of wiring time are available and upto 100 hours of drilling time may be used. Each air-conditioner assembled may be sold for Rs. 2,000 profit and each fan assembled may be sold for Rs. 1,000 profit. Formulate this problem as an L.P.P. in order to maximize the profit.
Solve the following using graphical method :
Minimize :Z=3x+5y
`2x+3x>=12`
`-x+y<=3`
`x<=4,y>=3,x>=0,y>=0`
There are found jobs to be completed. Each job must go through machines M1 , M2 , M3 in the order M1 - M2 - M3. Processing time in hours is given below. Determine the optimal sequesnce and idle time for machine M1 .
| Jobs | A | B | C | D |
| M1 | 5 | 8 | 7 | 3 |
| M2 | 6 | 7 | 2 | 5 |
| M3 | 7 | 8 | 10 | 9 |
Compute CDR using the information given below :
| Age group ( Years ) |
0-15 | 15-35 | 35-65 | 65 and above |
| Population | 9000 | 25000 | 32000 | 9000 |
Total number of deaths in a year is given to be 900.
Calculate the CDR for District A and B and compare them:
| Age group (in years) | District A | District B | ||
| No.of. persons (in '000) |
No.of. deaths |
No.of. persons (in '000) |
No.of. deaths | |
| 0 - 15 | 1 | 20 | 2 | 50 |
| 15 - 60 | 3 | 30 | 7 | 70 |
| 60 and above | 2 | 40 | 1 | 25 |
Diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1500 calories Two foods F1 and F2 cost Rs. 50 and Rs. 75 per unit respectively. Each unit of food F1 contains 200 units of vitamins, 1 unit of minerals and 40 calories, whereas each unit of food F2 contains 100 units of vitamins, 2 units of minerals and 30 calories. Formulate the above problem as L.P.P. to satisfy the sick person's requirements at minimum cost.
Minimize: Z = 2x + y
Subject to: x + y ≤ 5
x + 2y ≤ 8
4x + 3y ≥ 12
x ≥ o, y ≥ o
Solve graphically.
Find the graphical solution for the following system of linear equations :
3x + 4y ≥ 12 , 4x + 7y ≤ 28 , y ≥ 1 , x ≥ 0 , y ≥ 0 ,
Hence find the co-ordinates of comer points of the common region.
Find the graphical solution for following system of linear inequations
`"x"_1/60 + "x"_2/90 <= 1 ; 5x_1 + 8x_2 ≤ 600 , x_1 ≥ 0 , x_2 ≥ 0`
Solve the following L.P.P.:
Maximize Z = 4x + 5y
subject to 2x + y ≥ 4
x + y ≤ 5,
0 ≤ x ≤ 3,
0 ≤ y ≤ 3
Solve the following L.P.P. graphically Minimize Z = 3x + 5y Subject to 2x + 3y ≥ 12
-x + y ≤ 3
x ≤ 4
y ≥ 3
A person makes two types of gift items A and B requiring the services of a cutter and a finisher. Gift item A requires 4 hours of the cutter's time and 2 hours of finisher's time. Fifth item B requires 2 hours of the cutter's time and 4 hours of finisher's time. The cutter and finisher have 208 hours and 152 hours available time respectively every month. The profit on one gift item of type A is ₹ 75 and on one gift item of type, B is ₹ 125. Assuming that the person can sell all the gift items produced, determine how many gift items of each type should he make every month to obtain the best returns?
Find common region for the following system of linear inequations :
x ≥ -3, 4x - 5y ≥ -20, 3x + 4y ≤ 12, y ≥ -2
Solve the following L.P.P. :
Minimize : Z = 4x + 10y,
Subject to : 2x + 5y ≤10 , 5x + 3y ≤ 15,
x + 2y ≥ 30, x ≥ 0, y ≥ 0.
