Advertisements
Advertisements
Question
Multiply:
\[\frac{- 6}{11} \text{by} \frac{- 55}{36}\]
Sum
Solution
\[\frac{- 6}{11} \times \frac{- 55}{36} = \frac{- 6}{11} \times \frac{- 5 \times 11}{6 \times 6} = \frac{5}{6}\]
shaalaa.com
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
Simplify:
\[\frac{- 8}{19} + \frac{- 4}{57}\]
Subtract the first rational number from the second in each of the following:
\[\frac{3}{8}, \frac{5}{8}\]
Evaluate each of the following:
\[\frac{4}{7} - \frac{- 5}{- 7}\]
Express each of the following as a rational number of the form \[\frac{p}{q}:\]
\[\frac{- 7}{4} + 0 + \frac{- 9}{5} + \frac{19}{10} + \frac{11}{14}\]
Multiply:
\[- \frac{15}{11} \text{by} 7\]
Simplify each of the following and express the result as a rational number in standard form:
\[\frac{- 16}{21} \times \frac{14}{5}\]
Simplify:
\[\left( \frac{3}{11} \times \frac{5}{6} \right) - \left( \frac{9}{12} \times \frac{4}{3} \right) + \left( \frac{5}{13} \times \frac{6}{15} \right)\]
Divide:
\[5 \text{by} \frac{- 5}{7}\]
The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
| Golden eagle | Blue jay |
 |
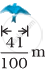 |
How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay?
If `p/q` is a rational number, then q cannot be ______.
