Advertisements
Advertisements
Question
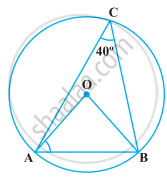
निम्नलिखित आकृति में, ∠ACB = 40° है। ∠OAB ज्ञात कीजिए।
Solution
दिया गया है, ∠ACB = 40°
हम जानते हैं कि, एक वृत्तखंड वृत्त पर एक कोण अंतरित करता है जो केंद्र पर अंतरित कोण का आधा होता है।
∴ ∠AOB = 2∠ACB
⇒ `∠ACB = (∠AOB)/2`
⇒ 40° = `1/2`∠AOB
⇒ ∠AOB = 80° ...(i) [दोनों एक वृत्त की त्रिज्या हैं।]
∆AOB में, AO = BO
⇒ ∠OBA = ∠OAB ...(ii) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
हम जानते हैं कि, त्रिभुज AOB के तीनों कोणों का योग 180° होता है।
∴ ∠AOB + ∠OBA + ∠OAB = 180°
⇒ 80° + ∠OAB + ∠OAB = 180° ...[समीकरण (i) और (ii) से]
⇒ 2∠OAB = 180° – 80°
⇒ 2∠OAB = 100°
∴ ∠OAB = `100^circ/2` = 50°
APPEARS IN
RELATED QUESTIONS
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
वृत्तखंड एक चाप तथा ______ के बीच का भाग होता है।
त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
संलग्न आकृति देखकर लिखिए:

एक व्यास
संलग्न आकृति देखकर लिखिए:
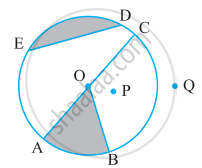
बहिर्भाग में एक बिंदु
कोई वृत खींचिए और निम्न को अंकित कीजिए:
-
उसका केंद्र
-
एक वृतखंड
-
एक त्रिज्या
-
उसके अभ्यंतर में एक बिंदु
-
एक व्यास
-
उसके बहिर्भाग में एक बिंदु
-
एक त्रिज्यखंड
- एक चाप
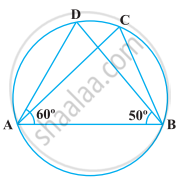
निम्नलिखित आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
चाँदे का प्रयोग किए बिना, दो न्यूनकोण और एक अधिक कोण खींचिए। इन कोणों की मापों का आकलन कीजिए। इनको चाँदे से मापिए और देखिए कि आपका आकलन कितना सही है।
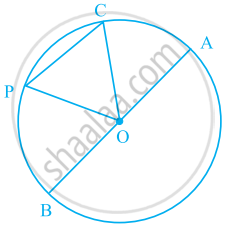
आकृति में O एक वृत्त का केंद्र है। CP द्वारा बनने वाले वृत्त के लघु वृत्तखंड को छायांकित कीजिए।
एक वृत्त की त्रिज्या 10 सेमी तथा जीवा की केंद्र से दूरी 6 सेमी है तो उस जीवा की लंबाई कितनी होगी?
