Advertisements
Advertisements
प्रश्न
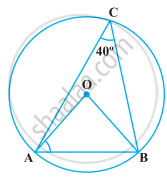
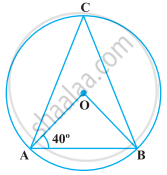
निम्नलिखित आकृति में, ∠ACB = 40° है। ∠OAB ज्ञात कीजिए।
उत्तर
दिया गया है, ∠ACB = 40°
हम जानते हैं कि, एक वृत्तखंड वृत्त पर एक कोण अंतरित करता है जो केंद्र पर अंतरित कोण का आधा होता है।
∴ ∠AOB = 2∠ACB
⇒ `∠ACB = (∠AOB)/2`
⇒ 40° = `1/2`∠AOB
⇒ ∠AOB = 80° ...(i) [दोनों एक वृत्त की त्रिज्या हैं।]
∆AOB में, AO = BO
⇒ ∠OBA = ∠OAB ...(ii) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
हम जानते हैं कि, त्रिभुज AOB के तीनों कोणों का योग 180° होता है।
∴ ∠AOB + ∠OBA + ∠OAB = 180°
⇒ 80° + ∠OAB + ∠OAB = 180° ...[समीकरण (i) और (ii) से]
⇒ 2∠OAB = 180° – 80°
⇒ 2∠OAB = 100°
∴ ∠OAB = `100^circ/2` = 50°
APPEARS IN
संबंधित प्रश्न
वृत्त की सबसे बड़ी जीवा वृत्त का _____ होता है।
वृत्तखंड एक चाप तथा ______ के बीच का भाग होता है।
एक वृत्त में समान लंबाई की परिमित जीवाएँ होती हैं।
संलग्न आकृति देखकर लिखिए:
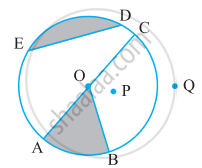
तीन त्रिज्याएँ
संलग्न आकृति देखकर लिखिए:
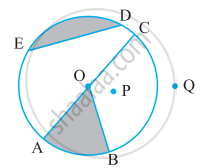
अभ्यंतर में दो बिंदु
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
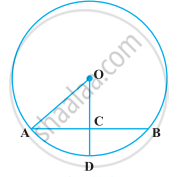
निम्नलिखित आकृति में, यदि OA = 5 cm, AB = 8 cm तथा OD जीवा AB पर लंब है, तो CD बराबर है
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
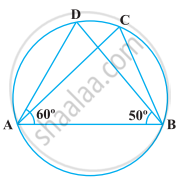
निम्नलिखित आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
यदि एक वृत्त PXAQBY की एक जीवा AB का लंब समद्विभाजक वृत्त को P और Q बिंदुओं पर प्रतिच्छेद करता है, तो सिद्ध कीजिए कि चाप PXA ≅ चाप PYB हैं।
