Advertisements
Advertisements
Question
निम्नलिखित तालिका के प्रत्येक स्तंभ में एक अनुपात दिया गया है इसके आधार पर अन्य दो अनुपात ज्ञात कीजिए तथा रिक्त स्थानों की पूर्ति कीजिए।
| sin θ | `11/61` | `1/2` | `3/5` | ||||||
| cos θ | `35/37` | `1/sqrt3` | |||||||
| tan θ | `1` | `21/20` | `8/15` | `1/(2sqrt2)` |
Solution
(i) cos θ = `35/37` ...(i)[दिया है]
समकोण ΔABC में,

∠C = θ
cos θ = `(θ" की संलग्न भुजा")/"कर्ण"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 35/37` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ BC = 35k and AC = 37k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ (37k)2 = AB2 + (35k)2
1369k2 = AB2 + 1225k2
AB2 = 1369k2 – 1225k2
AB2 = 144k2
AB2 = (12k)2
दोनों पक्षों का वर्गमूल निकालने पर,
AB = 12k
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = "12k"/"37k" = 12/37`
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा") = "AB"/"BC" = "12k"/"35k" = 12/35`
(ii) sin θ = `11/61` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ
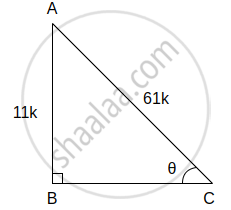
sin θ = `(θ "की सम्मुख भुजा")/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 11/61` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
AB = 11k and AC = 61k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ (61k)2 = (11k)2 + BC2
∴ 3721k2 = 121k2 + BC2
∴ BC2 = 3721k2 – 121k2
∴ BC2 = 3600k2
∴ BC2 = (60k)2
दोनों पक्षों का वर्गमूल निकालने पर,
BC = 60k
∴ cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = "60k"/"61k" = 60/61`
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा") = "AB"/"BC" = "11k"/"60k" = 11/60`
(iii) tan θ = 1 ...(i) [दिया है]
समकोण ΔABC में, ∠C = θ

tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा")`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/1` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 1k and BC = 1k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ AC2 = k2 + k2
∴ AC2 = 2k2
दोनों पक्षों का वर्गमूल निकालने पर,
∴ AC = `sqrt2k`
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
∴ cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
(iv) sin θ = `1/2` ... (i)[दिया है]
समकोण ΔABC में, ∠C = θ
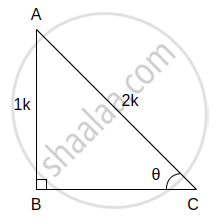
sin θ = `(θ "की सम्मुख भुजा")/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 1/2` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 1k and AC = 2k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ (2k)2 = k2 + BC2
∴ 4k2 = k2 + BC2
∴ BC2 = 4k2 – k2
∴ BC2 = 3k2
दोनों पक्षों का वर्गमूल निकालने पर,
∴ BC = `sqrt3k`
∴ cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = (sqrt3"k")/(2"k") = (sqrt3)/2`
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा") = "AB"/"BC" = (1"k")/(sqrt3"k") = 1/sqrt3`
(v) cos θ = `1/sqrt3` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ
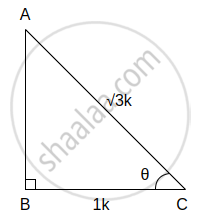
∴ cos θ = `(θ "की संलग्न भुजा")/"कर्ण"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 1/sqrt3` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ `"AB" = 1"k" and "BC" = sqrt3"k"`
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
`∴ (sqrt3"k")^2 = "AB"^2 + "k"^2`
∴ 3k2 = AB2 – k2
∴ AB2 = 3k2 – k2
∴ AB2 = 2k2
दोनों पक्षों का वर्गमूल निकालने पर,
AB = `sqrt2`k
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = (sqrt2"k")/(sqrt3"k") = sqrt2/sqrt3`
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा") = "AB"/"BC" = (sqrt2"k")/(1"k") = sqrt2`
(vi) tan θ = `21/20` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ
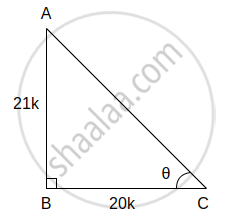
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा")`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 21/20` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 21k and BC = 20k.
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
AC2 = (21k)2 + (20k)2
AC2 = 441k2 + 400k2
AC2 = (841k)2
दोनों पक्षों का वर्गमूल निकालने पर,
AC = 29k
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = (21"k")/(29"k") = 21/29`
cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = (20"k")/(29"k") = 20/29`
(vii) tan θ = `8/15` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ

tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा")`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 8/15` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 8k and BC = 15k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ AC2 = (8k)2 + (15k)2
∴ AC2 = 64k2 + 225k2
∴ AC2 = (289k)2
दोनों पक्षों का वर्गमूल निकालने पर,
∴ AC = 17k
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = (8"k")/(17"k") = 8/17`
cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = (15"k")/(17"k") = 15/17`
(viii) sin θ = `3/5` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ
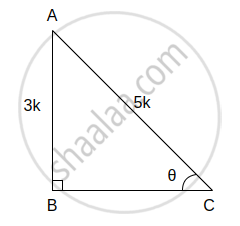
sin θ = `(θ "की सम्मुख भुजा")/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 3/5` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 3k and AC = 5k
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ (5k)2 = (3k)2 + BC2
∴ 25k2 = 9k2 + BC2
∴ BC2 = 25k2 – 9k2
∴ BC2 = 16k2
दोनों पक्षों का वर्गमूल निकालने पर,
∴ BC = 4k
∴ cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = (4"k")/(5"k") = 4/5`
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा") = "AB"/"BC" = (3"k")/(4"k") = 3/4`
(ix) tan θ = `1/(2sqrt2)` ...(i)[दिया है]
समकोण ΔABC में, ∠C = θ.
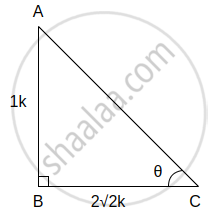
tan θ = `(θ "की सम्मुख भुजा")/(θ "की संलग्न भुजा")`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/(2sqrt2)` ...[(i) और (ii) से]
दोनो पक्षों में K से गुणा करने पर,
∴ AB = 1k and BC = `2sqrt2"k"`
अब, AC2 = AB2 + BC2 ...[पायथागोरस के प्रमेय]
∴ `"AC"^2 = (1"k")^2 + (2sqrt2"k")^2 `
∴ AC2 = 1k2 + 8k2
∴ AC2 = (9k)2
दोनों पक्षों का वर्गमूल निकालने पर,
∴ AC = 3k
∴ sin θ = `(θ "की सम्मुख भुजा")/"कर्ण" = "AB"/"AC" = (1"k")/(3"k") = 1/3`
cos θ = `(θ "की संलग्न भुजा")/"कर्ण" = "BC"/"AC" = (2sqrt2"k")/(3"k") = (2sqrt2)/3`
पूर्ण की गई तालिका नीचे दी गई है :
| sin θ | `12/37` | `11/61` | `1/sqrt2` | `1/2` | `sqrt2/sqrt3` | `21/29` | `8/17` | `3/5` | `1/3` |
| cos θ | `35/37` | `60/61` | `1/sqrt2` | `sqrt3/2` | `1/sqrt3` | `20/29` | `15/17` | `4/5` | `(2sqrt2)/3` |
| tan θ | `12/35` | `11/60` | 1 | `1/sqrt3` | `sqrt2` | `21/20` | `8/15` | `3/4` | `1/(2sqrt2)` |
APPEARS IN
RELATED QUESTIONS
ΔABC में जिसका कोण B समकोण है, AB = 24 cm, BC = 7 cm है। निम्नलिखित का मान ज्ञात कीजिए:
sin A, cos A
ΔABC में जिसका कोण B समकोण है, AB = 24 cm, BC = 7 cm है। निम्नलिखित का मान ज्ञात कीजिए:
sin C, cos C
यदि sec θ = `13/12`, हो तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
यदि ∠A और ∠B न्यून कोण हो, जहाँ cos A = cos B, तो दर्शाइए कि ∠A = ∠B
यदि cot θ = `7/8`, cot2 θ का मान निकालिए।
बताइए की निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
बताइए की निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
किसी भी कोण θ के लिए sin θ `4/3`
व्यंजक `[(sin^2 22^circ + sin^2 68^circ)/(cos^2 22^circ + cos^2 68^circ) + sin^2 63^circ + cos 63^circ sin 27^circ]` का मान ______ है।
व्यंजक (sin 80° – cos 80°) का मान ऋणात्मक है।
sin20° = cos ______°
