Question

यदि ∠A और ∠B न्यून कोण हो, जहाँ cos A = cos B, तो दर्शाइए कि ∠A = ∠B

Answer 1

माना एक त्रिभुज ABC पर विचार करें जिसमें CD ⊥ AB है।

दिया जाता है कि

cos A = cos B

⇒ `("AD")/("AC") = ("BD")/("BC")`       ...(1)

हमें ∠A = ∠B को सिद्ध करना है।

इसे सिद्ध करने के लिए, आइए AC को P तक इस प्रकार बढ़ाएँ कि BC = CP हो।

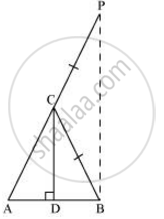
समीकरण (1) से, हम प्राप्त करते हैं

`("AB")/("BD") = ("AC")/("BC")`

⇒ `("AD")/("BD") = ("AC")/("CP")`        ..(निर्माण से, हमारे पास है BC = CP)         ...(2)

B.P.T, के विलोम का प्रयोग करके

CD || BP

⇒ ∠ACD = ∠CPB               ...(सभी तरीके से)                …(3)

And, ∠BCD = ∠CBP          ...(वैकल्पिक आंतरिक कोण)              …(4)

निर्माण से, हमारे पास है BC = CP

∴ ∠CBP = ∠CPB                ...(त्रिभुज की समान भुजाओं का सम्मुख कोण)         ...(5)

समीकरण (3), (4) और (5) से, हम प्राप्त करते हैं

∠ACD = ∠BCD            …(6)

In ΔCAD and ΔCBD,

∠ACD = ∠BCD              ...[समीकरण का उपयोग करना (6)]

∠CDA = ∠CDB                ...[Both 90°]

इसलिए, शेष कोण बराबर होने चाहिए।

∴ ∠CAD = ∠CBD

⇒ ∠A = ∠B

वैकल्पिक रूप से,

माना एक त्रिभुज ABC पर विचार करें जिसमें CD ⊥ AB है।

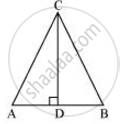
दिया जाता है कि,

cos A = cos B

⇒ `("AD")/("AC") = ("AC")/("BC")`

⇒ `("AD")/("BD") = ("AC")/("BC")`

माना `("AD")/("BD") = ("AC")/("BC") = k`

⇒ AD = k BD                 …(1)

और, AC = k BC               …(2)

त्रिभुज CAD और CBD के लिए पाइथागोरस प्रमेय का उपयोग करते हुए, हम प्राप्त करते हैं

CD² = AC² − AD²                  …(3)

And, CD² = BC² − BD²               …(4)

समीकरण (3) और (4) से, हम प्राप्त करते हैं

AC² − AD² = BC² − BD²

⇒ (k BC)² − (k BD)² = BC² − BD²

⇒ k² (BC² − BD²) = BC² − BD²

⇒ k² = 1

⇒ k = 1

इस मान को समीकरण (2) में रखने पर, हम प्राप्त करते हैं

AC = BC

⇒ ∠A = ∠B          ...(त्रिभुज की समान भुजाओं के सम्मुख कोण)

Answer 2

∠A और ∠B न्यूनकोण हैं

Cos A = cos B S.T ∠A = ∠B

समकोण त्रिभुज ACB

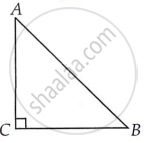
cos A= `("AC")/("AB")`

cos B = `("BC")/("AB")`

cos A = cos B

`("AC")/("AB") = ("BC")/("AB")`

AC = BC

∠A = ∠B