Advertisements
Advertisements
Question
Obtain an expression for the angular momentum of a body rotating with uniform angular velocity.
Solution
- Consider a rigid object rotating with a constant angular speed ‘ω’ about an axis perpendicular to the plane of the paper.
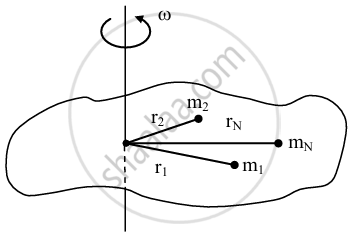
A body of N particles - Let us consider the object to consist of N number of particles of masses m1, m2, …..mN at respective perpendicular distances r1, r2, …..rN from the axis of rotation.
- As the object rotates, all these particles perform UCM with the same angular speed ω, but with different linear speeds
v1 = r1 ω, v2 = r2 ω, .....vN = rN ω.
Directions of individual velocities `vecv_1, vecv_2, .......vecv_N,` are along the tangents to the irrespective tracks. - Linear momentum of the first particle is of magnitude p1 = m1v1 = m1r1ω. Its direction is along that of `vecv_1.`
Its angular momentum is thus of magnitude L1 = p1r1 = `m_1r_1^2omega`
Similarly, `L_2 = m_2r_2^2 ω`, `L_3 = m_3r_3^2ω`, …., `L_N = m_Nr_N^2 ω`. - For a rigid body with a fixed axis of rotation, all these angular momenta are directed along the axis of rotation, and this direction can be obtained by using the right-hand thumb rule.
As all of them have the same direction, their magnitudes can be algebraically added. - Thus, the magnitude of angular momentum of the body is given by
`L = m_1r_1^2omega + m_1r_2^2omega + .... + m_Nr_N^2omega`
= `(m_1r_1^2 + m_2r_2^2 + ...... + m_Nr_N^2)omega = Iomega`
where `I = m_1r_1^2 + m_2r_2^2 + .... + m_Nr_N^2` is the moment of inertia of the body about the given axis of rotation.
APPEARS IN
RELATED QUESTIONS
State and prove: Law of conservation of angular momentum.
Answer in brief:
Derive an expression which relates angular momentum with the angular velocity of a rigid body.
The angular momentum of a system of particles is conserved ______
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity `omega`. Two objects of mass m are attached gently to the opposite ends of diameter of the ring. The wheel will now rotate with angular velocity ______.
If the radius of earth contracts to half of its value today, (the mass remaining unchanged), then the duration of the day will be ____________.
A ceiling fan having a moment of inertia 2 kg-m2 attains its maximum frequency of 60 rpm in ‘2π’ seconds. Calculate its power rating.
Which physical quantity of an atomic electron has the dimensions same as that of h?
