Advertisements
Advertisements
Question
Derive an expression for the difference in tensions at the highest and lowest point for a particle performing the vertical circular motion.
Solution
- Suppose a body of mass ‘m’ performs V.C.M on a circle of radius r as shown in the figure.
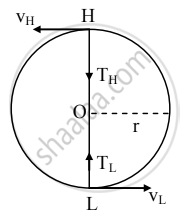
- Let,
TL = tension at the lowest point
TH = tension at the highest point
vL = velocity at the lowest point
vH = velocity at the highest point - At lowest point L,
TL = `("mv"_"L"^2)/"r" + "mg"` ….......(1)
At highest point H,
TH = `("mv"_"H"^2)/"r" - "mg"` ….......(2) - Subtracting (1) by (2),
TL - TH = `("mv"_"L"^2)/"r" + "mg" - (("mv"_"H"^2)/"r" - "mg")`
= `"m"/"r"("v"_"L"^2 - "v"_"H"^2) + 2"mg"`
∴ TL - TH = `"m"/"r"("v"_"L"^2 - "v"_"H"^2) + 2"mg"` ….......(3) - By law of conservation of energy,
(P.E + K.E) at L = (P.E + K.E) at H
∴ `0 + 1/2"mv"_"L"^2 = "mg".2"r" + 1/2"mv"_"H"^2`
∴ `1/2"m"("v"_"L"^2 - "v"_"H"^2) = "mg.2r"`
∴ `"v"_"L"^2 - "v"_"H"^2 = 4"gr"` .......(4) - From equation (3) and (4),
TL − TH = `"m"/"r"(4"gr") + 2"mg"` = 4mg + 2mg
∴ TL − TH = 6mg
APPEARS IN
RELATED QUESTIONS
A motorcyclist (as a particle) is undergoing vertical circles inside a sphere of death. The speed of the motorcycle varies between 6 m/s and 10 m/s. Calculate the diameter of the sphere of death. How much minimum values are possible for these two speeds?
The equiconvex lens has a focal length 'f'. If the lens is cut along the line perpendicular to the principal axis and passing through the pole, what will be the focal length of any half part?
The maximum and minimum tensions in the string whirling in a circle of radius 2.5 m with constant velocity are in the ratio 5 : 3. Then its velocity is ____________.
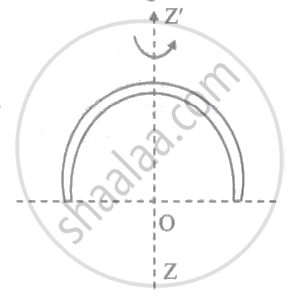
Consider a uniform semicircular wire of mass M and radius R as shown in the figure. Its M.I. about an axis ZZ' is ____________.
A particle is given an initial speed u inside a smooth spherical shell of radius R = 1 m so that it is just able to complete the circle. Acceleration of the particle when it is in vertical circle is ____________.
Consider a particle of mass m suspended by a string at the equator. Let R and M denote radius and mass of the earth. If ω is the angular velocity of rotation of the earth about its own axis, then the tension on the string will be (cos 0° = 1).
A rod of length 'L' is hung from its one end and a mass 'm' is attached to its free end. What tangential velocity must be imparted to 'm'. so that it reaches the top of the vertical circle? (g = acceleration due to gravity)
A ferris wheel with radius 20 m makes 1 revolution in every 10 s. The force exerted by the passenger of weight 55 kg on the seat, when he is at the top of the ferris wheel, is ____________.
A body of mass 0.5 kg is rotating in a vertical circle of radius 2 m. What will be the difference in its kinetic energy at the top and bottom of the circle? (Take g = 9.8 m/s2)
A particle of mass 'm' is rotating in a horizontal circle of radius 'r' with unifom1 velocity `vec"V"`. The change in its momentum at two diametrically opposite points will be ______.
A particle is performing vertical circular motion. The difference in tension at lowest and highest point is ______.
A sphere of mass 'M' is attached to one end of a metal wire having length 'L' and diameter 'D'. It is whirled in a vertical circle of radius R with angular velocity 'ω'. When the sphere is at lowest point of its path, the elongation of the wire is ______.
(Y= Young's modulus of the material of the wire, g =acceleration due to gravity)
A thin, uniform metal rod of mass 'M' and length 'L' is swinging about a horizontal axis passing through its end. Its maximum angular velocity is 'ω'. Its centre of mass rises to a maximum height of ______.
(g =acceleration due to gravity)
A mass m is revolving in a vertical circle at the end of a string of length 20 cm. By how much does the tension of the string at the lowest point exceed the tension at the topmost point?
Derive expressions for the linear velocity at the lowest position, mid-way position and top-most position for a particle revolving in a vertical circle, if it has to just complete circular motion without string slackening at the top.
A motor cyclist rides in a vertical hollow sphere of radius 5 m. Find minimum angular speed required so that it does not loose contact with the sphere at the highest point. (g = 9.8m/s2)
