Advertisements
Advertisements
Question
Derive expressions for the linear velocity at the lowest position, mid-way position and top-most position for a particle revolving in a vertical circle, if it has to just complete circular motion without string slackening at the top.
Solution
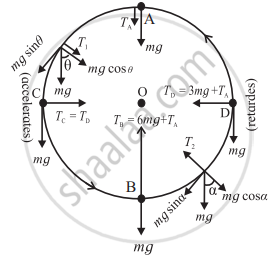
Vertical circular motion
Consider a bob (treated as a point mass) tied to a (practically) massless, inextensible and flexible string. It is whirled along a vertical circle so that the bob performs a vertical circular motion and the string rotates in a vertical plane. At any position of the bob, there are only two forces acting on the bob:
- Its weight is mg, vertically downwards, which is constant.
- The force due to the tension along the string is directed along the string and towards the centre. Its magnitude changes periodically with time and location.
Top-most position (A):
Force due to tension in the string and mg are both in the same direction (downward).
∴ TA + mg = `(m"v"_A^2)/r`
At the topmost position, A, the tension in the string is 0.
∴ TA = 0
∴ mg = `(m"v"_A^2)/r`
∴ `("v"_A)_"min" = sqrt(rg)` ....(i)
Lower-most position (B):
Force due to tension in the string is in an upward direction towards the center and opposite to the direction of mg.
∴ TB - mg = `(m"v"_B^2)/r`
While moving down from the uppermost to the lowermost point, the gravitational potential energy is converted into kinetic energy because the motion is governed only by gravity.
∴ mg(2r) = `1/2m"v"_B^2 - 1/2m"v"_A^2`
∴ `"v"_B^2 - "v"_A^2 = 4rg`
∴ `"v"_B^2 - rg = 4rg` .............[from (i)]
∴ `("v"_B)_"min" = sqrt(5rg)` ....(ii)
Mid-way Positions (C and D):
Let vC be the velocity at point C.
Total energy at point C = Kinetic energy + Potential Energy
= `1/2m"v"_C^2 + mgr`
Total energy at point B = Kinetic energy + Potential Energy
= `1/2m"v"_B^2 + 0 = 5/2 mgr` ....[From (ii)]
From the law of conservation of energy,
Total energy at point C = Total energy at point B
∴ `1/2m"v"_C^2 + mgr = 5/2mgr`
∴ `"v"_C^2 + 2rg = 5rg`
∴ `("v"_C)_"min" = sqrt(3rg)`
APPEARS IN
RELATED QUESTIONS
A motorcyclist (as a particle) is undergoing vertical circles inside a sphere of death. The speed of the motorcycle varies between 6 m/s and 10 m/s. Calculate the diameter of the sphere of death. How much minimum values are possible for these two speeds?
Derive an expression for the difference in tensions at the highest and lowest point for a particle performing the vertical circular motion.
The maximum and minimum tensions in the string whirling in a circle of radius 2.5 m with constant velocity are in the ratio 5 : 3. Then its velocity is ____________.
A particle is given an initial speed u inside a smooth spherical shell of radius R = 1 m so that it is just able to complete the circle. Acceleration of the particle when it is in vertical circle is ____________.
A rod of length 'L' is hung from its one end and a mass 'm' is attached to its free end. What tangential velocity must be imparted to 'm'. so that it reaches the top of the vertical circle? (g = acceleration due to gravity)
A ferris wheel with radius 20 m makes 1 revolution in every 10 s. The force exerted by the passenger of weight 55 kg on the seat, when he is at the top of the ferris wheel, is ____________.
A body of mass 0.5 kg is rotating in a vertical circle of radius 2 m. What will be the difference in its kinetic energy at the top and bottom of the circle? (Take g = 9.8 m/s2)
A particle of mass 'm' is rotating in a horizontal circle of radius 'r' with unifom1 velocity `vec"V"`. The change in its momentum at two diametrically opposite points will be ______.
A particle is performing vertical circular motion. The difference in tension at lowest and highest point is ______.
A sphere of mass 'M' is attached to one end of a metal wire having length 'L' and diameter 'D'. It is whirled in a vertical circle of radius R with angular velocity 'ω'. When the sphere is at lowest point of its path, the elongation of the wire is ______.
(Y= Young's modulus of the material of the wire, g =acceleration due to gravity)
A stone is tied at the end of a rope of length 1 m and whirled in a vertical circle. The ratio of velocity at highest point to lowest point will be ______.
A thin, uniform metal rod of mass 'M' and length 'L' is swinging about a horizontal axis passing through its end. Its maximum angular velocity is 'ω'. Its centre of mass rises to a maximum height of ______.
(g =acceleration due to gravity)
When the bob performs a vertical circular motion and the string rotates in a vertical plane, the difference in the tension in the string at horizontal position and uppermost position is ______.
A mass m is revolving in a vertical circle at the end of a string of length 20 cm. By how much does the tension of the string at the lowest point exceed the tension at the topmost point?
In vertical circular motion, the ratio of kinetic energy of a particle at highest point to that at lowest point is ______.
A motor cyclist rides in a vertical hollow sphere of radius 5 m. Find minimum angular speed required so that it does not loose contact with the sphere at the highest point. (g = 9.8m/s2)
Explain the term sphere of death.
