Advertisements
Advertisements
Question
Calculate the work done in blowing a soap bubble to a radius of 1 cm. The surface tension of soap solution is 2.5 × 10-2 N/m.
Solution
Given:
T = 2.5 × 10-2 N/m, r1 = 0 m, r2 = 1 cm = 10-2 m, W = ?
Formula:
W = 2T dA = 2T × 4π`(r_2^2 - r_1^2)`
∴ W = `2 xx 2.5 xx 10^-2 xx 4pi xx 10^-4`
∴ W = 6.283 × 10-5 J
APPEARS IN
RELATED QUESTIONS
Derive the relation between surface tension and surface energy per unit area.
Answer in one sentence.
State the SI unit and dimensions of stress.
The radius of a soap bubble is blown up to double its value under isothermal conditions. If 'r' be the initial radius of the bubble, and T be the surface tension, then energy spent in doubling the radius is ______
Assertion: If work done in increasing the size of a soap film from 10 cm x 4 cm to 10 cm x 8 cm is 2 x 10-4 J, then the surface tension is 5 x 10-4 N m-1.
Reason: Work done = Surface tension x increase in area.
If two identical mercury drops are combined to form a single drop, then its temperature will ____________.
Soap solution bubble having radius `1/sqrtπ` cm is expanded to a bubble of radius `4/sqrtπ`. If the surface tension of soap solution is 30 dyne/cm, then the work done is ______.
Two spherical soap bubbles of radii r1 and r2 in vacuum coalesce under isothermal conditions. The resulting bubble has a radius R such that ____________.
A liquid drop having surface energy 'E' is spread into 216 droplets of same size. The final surface energy of the droplets is ____________.
The surface energy of a liquid drop is u. If it is sprayed into 1000 equal droplets, then its surface energy becomes ______.
If a million tiny droplets of water of the same radius coalesce into one larger drop, then the ratio of the surface energy of the large drop to the total surface energy of all the droplets will be ____________.
On the surface of the liquid in equilibrium, molecules of the liquid possess ____________.
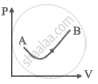
Consider a process shown in the figure. During this process, the work done by the system ______.
A fix number of spherical drops of a liquid of radius 'r' coalesce to form a large drop of radius 'R' and volume 'V'. If 'T' is the surface tension then energy ______.
A water film is formed between the two straight parallel wires, each of length 10 cm, kept at a separation of 0.5 cm. Now, the separation between them is increased by 1 mm without breaking the water film. The work done for this is ______.
(surface tension of water = 7.2 x 10-2Nm-1)
A metal coin of thickness 'd' and density 'ρ' is floating on water of surface tension 'T'. The radius of the coin is ______.
g = acceleration due to gravity
One thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy is ______.
The surface tension of a liquid is 10 N/m. If a thin film of the area 0.05 m2 is formed on a loop. Then the surface energy will be:
One cubic plate, having a 15 cm side, floats on water surface. If surface tension of water is 60 dyne/cm. To lift this plate from water, Find the extra force required against weight.
A water drop of diameter 2 cm is broken into 64 equal droplets. The surface tension of water is 0.075 N/m. In this process the gain in surface energy will be ______.
A big water drop is formed by the combination of 'n' small water drops of equal radii. The ratio of the surface energy of 'n 'drops to the surface energy of big drop is ______.
If T1, T2 and T3 are the forces due to surface tension at the liquid-s solid-gas and liquid-gas interfaces such that T2 - T1 ≅ T3 and the contact angle for the liquid-solid pair is θ then ______.
Calculate the amount of energy evolved when 343 droplets of mercury each of radius. 0.05 mm, combine to form one drop. The surface tension of mercury is 50 x 10-2 N/m.
