Advertisements
Advertisements
प्रश्न
Calculate the work done in blowing a soap bubble to a radius of 1 cm. The surface tension of soap solution is 2.5 × 10-2 N/m.
उत्तर
Given:
T = 2.5 × 10-2 N/m, r1 = 0 m, r2 = 1 cm = 10-2 m, W = ?
Formula:
W = 2T dA = 2T × 4π`(r_2^2 - r_1^2)`
∴ W = `2 xx 2.5 xx 10^-2 xx 4pi xx 10^-4`
∴ W = 6.283 × 10-5 J
APPEARS IN
संबंधित प्रश्न
Derive the relation between surface tension and surface energy per unit area.
Answer in one sentence.
State the SI unit and dimensions of stress.
The radius of a soap bubble is blown up to double its value under isothermal conditions. If 'r' be the initial radius of the bubble, and T be the surface tension, then energy spent in doubling the radius is ______
Energy needed in breaking a drop of radius R into n drops each of radius r is given by ____________.
If two identical mercury drops are combined to form a single drop, then its temperature will ____________.
Which one of the following statements is correct?
A metal wire of density 'p' floats on water surface horizontally. If it is NOT to sink in water then maximum radius of wire is proportional to ______.
(T = surface tension of water, g = gravitational acceleration)
Two spherical soap bubbles of radii r1 and r2 in vacuum coalesce under isothermal conditions. The resulting bubble has a radius R such that ____________.
If a million tiny droplets of water of the same radius coalesce into one larger drop, then the ratio of the surface energy of the large drop to the total surface energy of all the droplets will be ____________.
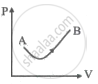
Consider a process shown in the figure. During this process, the work done by the system ______.
A fix number of spherical drops of a liquid of radius 'r' coalesce to form a large drop of radius 'R' and volume 'V'. If 'T' is the surface tension then energy ______.
A metal coin of thickness 'd' and density 'ρ' is floating on water of surface tension 'T'. The radius of the coin is ______.
g = acceleration due to gravity
One thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy is ______.
The surface tension of a liquid is 10 N/m. If a thin film of the area 0.05 m2 is formed on a loop. Then the surface energy will be:
A water drop of diameter 2 cm is broken into 64 equal droplets. The surface tension of water is 0.075 N/m. In this process the gain in surface energy will be ______.
A big water drop is formed by the combination of 'n' small water drops of equal radii. The ratio of the surface energy of 'n 'drops to the surface energy of big drop is ______.
If T1, T2 and T3 are the forces due to surface tension at the liquid-s solid-gas and liquid-gas interfaces such that T2 - T1 ≅ T3 and the contact angle for the liquid-solid pair is θ then ______.
Prove that, equivalent S.I. unit of surface tension is J/m2.
Define the surface energy of the liquid.
