Advertisements
Advertisements
Question
Obtain the expression for the instantaneous value of emf induced.
Solution
Consider a coil of M turns and area A being rotated at a constant angular velocity ω in a magnetic field of flux density B, its axis being perpendicular to the field.
When the normal to the coil is at an angle θ to the field, the flux through the coil is BAN cosθ = BAN cos(ω)t, since θ = ωt.
Figure 1:
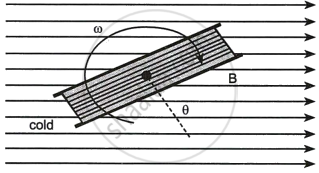
Figure 2:

`E = -(dphi)/(dt)`
`E = -(d(BAN costheta))/(dt)`
E = BAN ωsin(ωt)
The maximum value of the e.m.f. (E0) is when θ = ωt = 90° (that is, the coil in the plane of the field as shown in figure) and is given by
`E_0 = BANomega`
RELATED QUESTIONS
Draw a labelled diagram of an ac generator.
State the working of a.c. generator with the help of a labeled diagram.
The coil of an a.c. generator having N turns, each of area A, is rotated with a constant angular velocity ω. Deduce the expression for the alternating e.m.f. generated in the coil.
What is the source of energy generation in this device?
`20/pi^2`H inductor is connected to a capacitor of capacitance C. The value of C in order to impart maximum power at 50 Hz is
Give the principle of AC generator.
How are the three different emfs generated in a three-phase AC generator? Show the graphical representation of these three emfs.
A resistor, capacitor, and inductor are connected in series across an AC generator. Which of the following statements is false?
The average value of alternating current over a full cycle is always ______. [I0 = Peak value of current]
Briefly describe the working of ac generator.
Draw a schematic diagram of an AC generator.
An AC generator spinning at a rate of 750 rev/min produces a maximum emf of 45 V. At what angular speed does this generator produce a maximum emf of 120 V?
