Advertisements
Advertisements
Question
On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4 m when it is 6m away from the point of projection. Finally it reaches the ground 12 m away from the starting point. Find the angle of projection
Solution
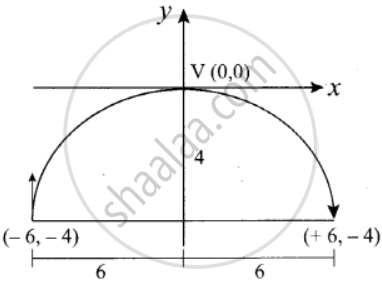
Equation of the parabola be x2 = – 4ay .......(1)
B(6, – 4) lies on parabola
62 = – 4a(– 4)
`36/16` = a
⇒ a = `9/4`
(1) ⇒ x2 = `- (9/4) y`
x2 = – 9y .......(2)
Now need tofind slope at (– 6, – 4)
Diff (2) w.r.to x
2x = `- 9 ("d"y)/("d"x)`
`("d"y)/("d"x) = (2x)/(-9)`
At(– 6, – 4), `("d"y)/("d"x) = (2(- 6))/(- 9)`
= `12/9`
= `4/3`
tan θ = `4/3`
θ = `tan^-1 (4/3)`
APPEARS IN
RELATED QUESTIONS
A bridge has a parabolic arch that is 10 m high in the centre and 30 m wide at the bottom. Find the height of the arch 6m from the centre, on either sides
A tunnel through a mountain for a four-lane highway is to have a elliptical opening. The total width of the highway (not the opening) is to be 16 m, and the height at the edge of the road must be sufficient for a truck 4 m high to clear if the highest point of the opening is to be 5 m approximately. How wide must the opening be?
At a water fountain, water attains a maximum height of 4 m at horizontal distance of 0.5 m from its origin. If the path of water is a parabola, find the height of water at a horizontal distance of 0.75 m from the point of origin.
An engineer designs a satellite dish with a parabolic cross-section. The dish is 5m wide at the opening, and the focus is placed 1 2. m from the vertex. Position a coordinate system with the origin at the vertex and the x-axis on the parabola’s axis of symmetry and find an equation of the parabola
An engineer designs a satellite dish with a parabolic cross-section. The dish is 5 m wide at the opening and the focus is placed 1.2 m from the vertex. Find the depth of the satellite dish at the vertex
A rod of length 1 2. m moves with its ends always touching the coordinate axes. The locus of a point P on the rod, which is 0 3. m from the end in contact with x-axis is an ellipse. Find the eccentricity
Assume that water issuing from the end of a horizontal pipe, 7 5. m above the ground, describes a parabolic path. The vertex of the parabolic path is at the end of the pipe. At a position 2 5. m below the line of the pipe, the flow of water has curved outward 3 m beyond the vertical line through the end of the pipe. How far beyond this vertical line will the water strike the ground?
Points A and B are 10 km apart and it is determined from the sound of an explosion heard at those points at different times that the location of the explosion is 6 km closer to A than B. Show that the location of the explosion is restricted to a particular curve and find an equation of it.
Choose the correct alternative:
An ellipse has OB as semi-minor axes, F and F’ its foci and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is
Choose the correct alternative:
The eccentricity of the ellipse (x – 3)2 + (y – 4)2 = `y^2/9` is
Choose the correct alternative:
The locus of a point whose distance from (– 2, 0) is `2/3` times its distance from the line x = `(-9)/2` is
Choose the correct alternative:
The values of m for which the line y = `"m"x + 2sqrt(5)` touches the hyperbola 16x2 – 9y2 = 144 are the roots of x2 – (a + b)x – 4 = 0, then the value of (a + b) is
