Advertisements
Advertisements
Question
One end of a V-tube containing mercury is connected to a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45° each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.
Solution
Consider the diagram shown below
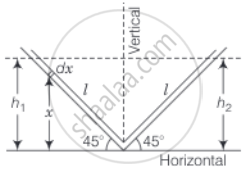
Let us consider an infinitesimal liquid column of length dx at a height x from the horizontal line.
If ρ = density of the liquid
A = cross-sectional area of V-tube
Pe of element dx will be given as PE = dmgx = (Aρdx)gx ......[∵ dm = pV = ρAdx]
Where Aρdx = dm = mass of element dx
∴ Total PE of the left column = `int_0^(h_1) Aρgxdx`
= `Aρg int_0^(h_1) x dx`
= `Aρg |x^2/2|_0^(h_1)`
= `Aρg h_1^2/2`
But, `h_1 = l sin 45^circ`
∴ PE = `(Aρg)/2 l^2 sin^2 45^circ` ......(i)
In a similar way,
PE of right column = `(Aρg)/2 l^2 sin^2 45^circ` ......(ii)
Total PE = `(Aρg)/2 l^2 sin^2 45^circ + (Aρg)/2 l^2 sin^2 45^circ`
= `2 xx 1/2 Aρgl^2 (1/sqrt(2))^2`
= `(Aρgl^2)/2` ......(iii)
If due to the pressure difference created y element of the left side moves on the right side, then liquid present in the left arm = l – y
Liquid present in the right arm = l + y
∴ Total PE = `Aρg(l - y)^2 sin62 45^circ + Aρg (l + y)^2 sin^2 45^circ`
Changes in PE = `(PE)_"final" - (PE)_"initial"`
or `ΔPE = (Aρg)/2 [(l - y)^2 + (l + y)^2 - l^2]`
= `(Aρg)/2 [l^2 + y^2 - 2ly + l^2 + y^2 + 2ly - l^2]`
= `(Aρg)/2 [2(l^2 + y^2)]`
= `Aρg(l^2 + y^2)` ........(iv)
If v is the change in velocity of the total liquid column, then the change in KE
`ΔKE = 1/2mv^2`
But `m = Aρ(2l)`
∴ `ΔKE = 1/2 Aρ2lv^2 = Aρlv^2` ......(v)
From equations (iv) and (v),
`ΔPE + ΔKE = Aρg(l^2 + y^2) + Aρlv^2` ......(vi)
The system is conservative.
∴ Change in total energy = 0
From equation (vi),
`Aρg(l^2 + y^2) + Aρlv^2` = 0
Differentiating both sides with respect to time (t), we get
`Aρg [0 + 2y (dy)/(dt)] + Aρl(2v) (dv)/(dt)` = 0
But, `(dy)/(dt) = v` and `(dv)/(dt) = a` ......[Acceleration]
⇒ `Aρg (2yv) + Aρl(2v)a` = 0
⇒ `(gy + la) 2Aρv` = 0
2Aρv = constant and 2Aρv ≠ 0
∴ `la + gy` = 0
`a + (g/l)y` = 0
or `(d^2y)/(dt^2) + (g/l)y` = 0
This is the standard differential equation for SHM of the form
`(d^2y)/(dt^2) + ω^2y` = 0
∴ `ω = sqrt(g/l)`
∴ T = `(2pi)/ω = 2pi sqrt(l/g)`
APPEARS IN
RELATED QUESTIONS
One end of a U-tube containing mercury is connected to a suction pump and the other end to the atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
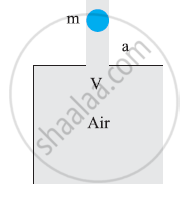
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.33). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal
Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
A circular disc of mass 10 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5 s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant α is defined by the relation J = –α θ, where J is the restoring couple and θ the angle of twist).
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is 0 cm.
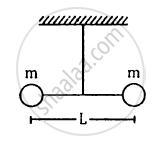
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the force exerted by the rod on one of the balls as the system passes through the mean position.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is 5 cm.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is 3 cm.
A mass M suspended from a light spring which is fixed at the upper end to rigid support oscillates in a vertical line with a period of 2 s. If the mass is increased by 20 g, then the time period of oscillation increases by 1 s. The value of M is ______.
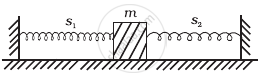
When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are ν1 and ν2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be ______.