Advertisements
Advertisements
Question
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
Solution
Consider the situation shown in the diagram.
The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the position of the particle. The external shells exert no force on the particle.
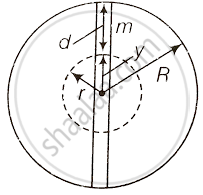
More clearly,
Let g' be the acceleration at P.
So, `g^' = g(1 - d/R) = g((R - d)/R)`
From the figure, `R - d = y`
⇒ `g^' = g y/R^'`
Force on the body at p,
F = `- mg^' = (- mg)/R y` .......(i)
⇒ F ∝ – y ......[Where y is the distance from the centre]
So, motion is S.H.M.
For time period, we can write equation (i)
As ma = `- (Mg)/Ry`
⇒ `a = - g/R y`
Comparing with a = `- ω^2y`
`ω^2 = g/R`
⇒ `((2pi)/T) = g/R`
⇒ T = `2pi sqrt(R/g)`
APPEARS IN
RELATED QUESTIONS
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
If the metal bob of a simple pendulum is replaced by a wooden bob of the same size, then its time period will.....................
- increase
- remain same
- decrease
- first increase and then decrease.
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Define practical simple pendulum
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
When will the motion of a simple pendulum be simple harmonic?
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
