Question

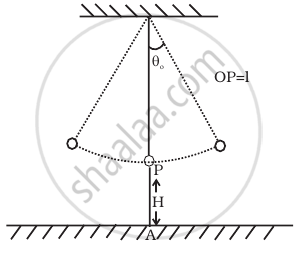
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ₀. The string snaps at θ = θ₀/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θ_o to be small so that sin θ_o = θ_o and cos θ_o = 1.

Answer 1

Consider the diagram,

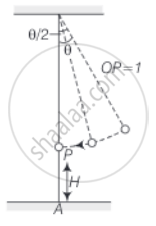
Let us assume t = 0 when θ_o = θ_o, then θ = θ₀ cos ωt

Given a seconds pendulum ω = 2π

⇒ θ = θ₀ cos 2πt  ......(i)

At time t₁ let θ = θ₀/2

∴ cos 2πt₁ = 1/2

⇒ `t_1 = 1/6`  ......`[∵ cos 2πt_1 = cos  π/3 = 2πt_1 = π/3]`

`(dθ)/(dt) = - (θ_0 2π) sin2πt`  .....[From equation (i)]

At `t = t_1 = 1/6`

`(dθ)/(dt) = - θ_0 2π sin  (2π)/6 = - sqrt(3)πθ_0`

A negative sign shows that it is going left.

Thus, the linear velocity is `u = - sqrt(3)πθ_0l` perpendicular to the string.

The vertical component is `u_y = - sqrt(3)πθ_0l sin (θ_0/2)`

And the horizontal component is `u_x = - sqrt(3)πθ_0l cos (θ_0/2)`

At the time it snaps, the vertical height is `H^' = H + l(1 - cos (θ_0/2))`  ......(ii)

Let the time required for fall be t, then `H^' = u_yt + (1/2)gt^2`   ......(Notice g is also in the negative direction)

or `1/2 gt^2 + sqrt(3)πθ_0l sin  θ_0/2 t - H^'` = 0

∴ t = `(-sqrt(3)πθ_0l sin  θ_0/2 +- sqrt(3π^2 θ_0^2 l^2 sin^2  θ_0/2 + 2gH^'))/g`

= `(-sqrt(3)πl θ_0^2/2 +- sqrt(3π^2 (θ_0^4/4)l^2 + 2gH^'))/g`  ......`[∵ sin  θ_0/2 ≃ θ_0/2 "for small angle"]`

Given that θ₀ is small, hence neglecting terms of order `θ_0^2` and higher

`t = sqrt((2H^')/g)`  .....[Fro, equation (iii)]

Now, `H^' = H + l(1 - 1)`  ......[∴ cos θ₀/2 = 1]

= H   .....[From equation (ii)]

⇒ t = `sqrt((2H)/g)`

The distance travelled in the x-direction is u_xt to the left of where the bob is snapped

X = U_xt = `sqrt(3) πθ_0l cos (θ_0/2) sqrt((2H)/g) s`

as θ₀ is small ⇒ `cos (θ_0/2)` = 1

X = `sqrt(3) πθ_0l sqrt((2H)/g) = sqrt((6H)/g) θ_0lπ`

At the time of snapping the bob was at a horizontal distance of `l sin (θ_0/2) = l  θ_0/2`  from A.

Thus, the distance of bob from A where it meets the ground is `(lθ_0)/2 - X = (lθ_0)/2 - sqrt((6H)/g) θ_0 lpi`

= `θ_0 l(1/2 - pi sqrt((6H)/g))`