Advertisements
Advertisements
प्रश्न
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
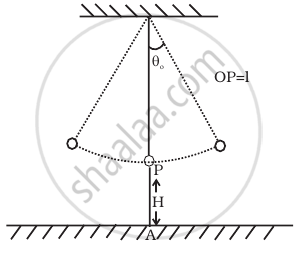
उत्तर
Consider the diagram,
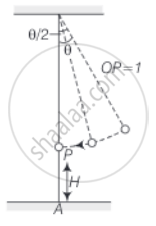
Let us assume t = 0 when θo = θo, then θ = θ0 cos ωt
Given a seconds pendulum ω = 2π
⇒ θ = θ0 cos 2πt ......(i)
At time t1 let θ = θ0/2
∴ cos 2πt1 = 1/2
⇒ `t_1 = 1/6` ......`[∵ cos 2πt_1 = cos π/3 = 2πt_1 = π/3]`
`(dθ)/(dt) = - (θ_0 2π) sin2πt` .....[From equation (i)]
At `t = t_1 = 1/6`
`(dθ)/(dt) = - θ_0 2π sin (2π)/6 = - sqrt(3)πθ_0`
A negative sign shows that it is going left.
Thus, the linear velocity is `u = - sqrt(3)πθ_0l` perpendicular to the string.
The vertical component is `u_y = - sqrt(3)πθ_0l sin (θ_0/2)`
And the horizontal component is `u_x = - sqrt(3)πθ_0l cos (θ_0/2)`
At the time it snaps, the vertical height is `H^' = H + l(1 - cos (θ_0/2))` ......(ii)
Let the time required for fall be t, then `H^' = u_yt + (1/2)gt^2` ......(Notice g is also in the negative direction)
or `1/2 gt^2 + sqrt(3)πθ_0l sin θ_0/2 t - H^'` = 0
∴ t = `(-sqrt(3)πθ_0l sin θ_0/2 +- sqrt(3π^2 θ_0^2 l^2 sin^2 θ_0/2 + 2gH^'))/g`
= `(-sqrt(3)πl θ_0^2/2 +- sqrt(3π^2 (θ_0^4/4)l^2 + 2gH^'))/g` ......`[∵ sin θ_0/2 ≃ θ_0/2 "for small angle"]`
Given that θ0 is small, hence neglecting terms of order `θ_0^2` and higher
`t = sqrt((2H^')/g)` .....[Fro, equation (iii)]
Now, `H^' = H + l(1 - 1)` ......[∴ cos θ0/2 = 1]
= H .....[From equation (ii)]
⇒ t = `sqrt((2H)/g)`
The distance travelled in the x-direction is uxt to the left of where the bob is snapped
X = Uxt = `sqrt(3) πθ_0l cos (θ_0/2) sqrt((2H)/g) s`
as θ0 is small ⇒ `cos (θ_0/2)` = 1
X = `sqrt(3) πθ_0l sqrt((2H)/g) = sqrt((6H)/g) θ_0lπ`
At the time of snapping the bob was at a horizontal distance of `l sin (θ_0/2) = l θ_0/2` from A.
Thus, the distance of bob from A where it meets the ground is `(lθ_0)/2 - X = (lθ_0)/2 - sqrt((6H)/g) θ_0 lpi`
= `θ_0 l(1/2 - pi sqrt((6H)/g))`
APPEARS IN
संबंधित प्रश्न
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
