Advertisements
Advertisements
प्रश्न
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
उत्तर १
Acceleration due to gravity on the surface of moon, g' = 1.7 m s–2
Acceleration due to gravity on the surface of earth, g = 9.8 m s–2
Time period of a simple pendulum on earth, T = 3.5 s
`T = 2pisqrt(1/g)`
Where l is the length of the pendulum
`:.l = T^2/(2pi)^2 xx g`
`=(3.5)^2/(4xx(3.14)^2) xx 9.8 m`
The length of the pendulum remains constant.
On moon’s surface, time period, `T' = 2pi sqrt(1/g^')`
`= 2pi sqrt(((3.5)^2/(4xx3.14)^2 xx 9.8)/1.7) = 8.4 s`
Hence, the time period of the simple pendulum on the surface of moon is 8.4 s.
उत्तर २
Here `g_m = 1.7 ms^(-2), g_e= 9.8 ms^2; T_m = ? T_e= 3.5 s^(-1)`
Since `T_e = 2pi sqrt(1/(g_e))` and `T_m = 2pisqrt(1/g_m)`
`:. T_m/T_e = sqrt(g_e/g_m) => T_m = T_e = sqrt(g_e/g_m)`
`= 3.5 sqrt(9.8/1.7) = 8.4 s`
उत्तर ३
Here `g_m = 1.7 ms^(-2), g_e= 9.8 ms^2; T_m = ? T_e= 3.5 s^(-1)`
Since `T_e = 2pi sqrt(1/(g_e))` and `T_m = 2pisqrt(1/g_m)`
`:. T_m/T_e = sqrt(g_e/g_m) => T_m = T_e = sqrt(g_e/g_m)`
`= 3.5 sqrt(9.8/1.7) = 8.4 s`
APPEARS IN
संबंधित प्रश्न
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Define practical simple pendulum
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
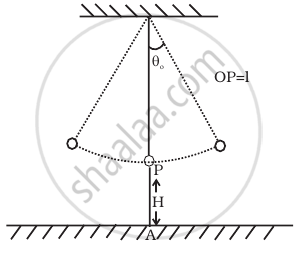
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
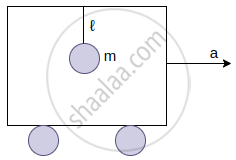
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)