Advertisements
Advertisements
प्रश्न
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
उत्तर १
Acceleration due to gravity on the surface of moon, g' = 1.7 m s–2
Acceleration due to gravity on the surface of earth, g = 9.8 m s–2
Time period of a simple pendulum on earth, T = 3.5 s
`T = 2pisqrt(1/g)`
Where l is the length of the pendulum
`:.l = T^2/(2pi)^2 xx g`
`=(3.5)^2/(4xx(3.14)^2) xx 9.8 m`
The length of the pendulum remains constant.
On moon’s surface, time period, `T' = 2pi sqrt(1/g^')`
`= 2pi sqrt(((3.5)^2/(4xx3.14)^2 xx 9.8)/1.7) = 8.4 s`
Hence, the time period of the simple pendulum on the surface of moon is 8.4 s.
उत्तर २
Here `g_m = 1.7 ms^(-2), g_e= 9.8 ms^2; T_m = ? T_e= 3.5 s^(-1)`
Since `T_e = 2pi sqrt(1/(g_e))` and `T_m = 2pisqrt(1/g_m)`
`:. T_m/T_e = sqrt(g_e/g_m) => T_m = T_e = sqrt(g_e/g_m)`
`= 3.5 sqrt(9.8/1.7) = 8.4 s`
उत्तर ३
Here `g_m = 1.7 ms^(-2), g_e= 9.8 ms^2; T_m = ? T_e= 3.5 s^(-1)`
Since `T_e = 2pi sqrt(1/(g_e))` and `T_m = 2pisqrt(1/g_m)`
`:. T_m/T_e = sqrt(g_e/g_m) => T_m = T_e = sqrt(g_e/g_m)`
`= 3.5 sqrt(9.8/1.7) = 8.4 s`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Define practical simple pendulum
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
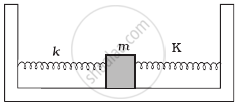
When will the motion of a simple pendulum be simple harmonic?
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
