Advertisements
Advertisements
प्रश्न
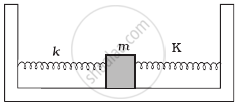
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
उत्तर
When the mass is displaced from the equilibrium position by a distance x towards the right, the right spring gets compressed by x developing a restoring force kx towards the left on the block. The left spring is stretched by an amount of x developing a restoring force kx left on the block.
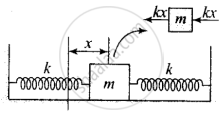
F1 = – kx (for left spring)
And F2 = – kx (for right spring)
Restoring force, F = F1 + F2 = – 2kx
∴ F = 2kx towards left.
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
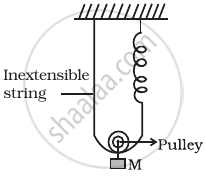
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
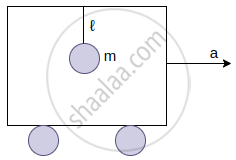
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)