Advertisements
Advertisements
प्रश्न
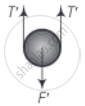
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
Advertisements
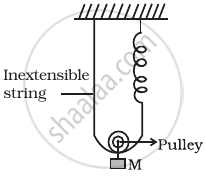
उत्तर
For the calculation purpose. in this situation, we will neglect gravity because it is constant throughout and will not affect the net restoring force.
Let in the equilibrium position, the spring has extended by an amount x0.
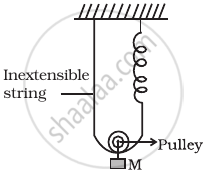
Now, if the mass is given a further displacement downwards by an amount of x. The string and spring both should increase in length by x.
But. string is inextensible, hence the spring alone will contribute the total extension x + x = 2x, to lower the mass down by x from the initial equilibrium mean position x0. So, net extension in the spring (= 2x + x0)
Now force on the mass before bullying (in the x0 extension case)
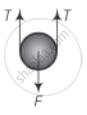
F = 2T
But T = kx0 ......[Where k is spring constant]
∴ F = 2kx0 ......(i)
When the mass is lowered further by x,
F' = 2T'
But new spring length = (2x + x0)
∴ F' = 2k(2x + x0) ......(ii)
Restoring force on the system
`F_"restoring" = - [F^' - F]`
Using equations (i) and (ii), we get
`F_"restoring" = -[2k(2x + x_0) - 2kx_0]`
= `- [2 xx 2kx + 2kx_0 - 2kx_0]`
= `- 4kx`
or Ma = `- 4kx`
Where, a = acceleration .....(As, F = ma)
⇒ a = `- ((4k)/M)x`
k, M is constant.
∴ a ∝ – x
Hence, the motion is S.H.M
Comparing the above acceleration expression with standard SHM equation a = – ω2x, we get
`ω^2 = (4k)/M`
⇒ `ω = sqrt((4K)/M)`
∴ Time period T = `(2pi)/ω = (2pi)/sqrt((4K)/M) = 2pi sqrt(M/(4k))`
APPEARS IN
संबंधित प्रश्न
If the metal bob of a simple pendulum is replaced by a wooden bob of the same size, then its time period will.....................
- increase
- remain same
- decrease
- first increase and then decrease.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Define practical simple pendulum
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
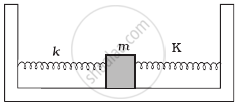
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
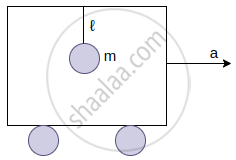
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
