Advertisements
Advertisements
Question
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
Advertisements
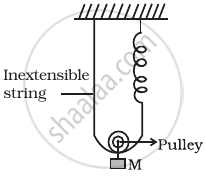
Solution
For the calculation purpose. in this situation, we will neglect gravity because it is constant throughout and will not affect the net restoring force.
Let in the equilibrium position, the spring has extended by an amount x0.
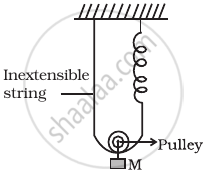
Now, if the mass is given a further displacement downwards by an amount of x. The string and spring both should increase in length by x.
But. string is inextensible, hence the spring alone will contribute the total extension x + x = 2x, to lower the mass down by x from the initial equilibrium mean position x0. So, net extension in the spring (= 2x + x0)
Now force on the mass before bullying (in the x0 extension case)
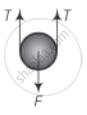
F = 2T
But T = kx0 ......[Where k is spring constant]
∴ F = 2kx0 ......(i)
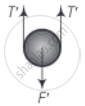
When the mass is lowered further by x,
F' = 2T'
But new spring length = (2x + x0)
∴ F' = 2k(2x + x0) ......(ii)
Restoring force on the system
`F_"restoring" = - [F^' - F]`
Using equations (i) and (ii), we get
`F_"restoring" = -[2k(2x + x_0) - 2kx_0]`
= `- [2 xx 2kx + 2kx_0 - 2kx_0]`
= `- 4kx`
or Ma = `- 4kx`
Where, a = acceleration .....(As, F = ma)
⇒ a = `- ((4k)/M)x`
k, M is constant.
∴ a ∝ – x
Hence, the motion is S.H.M
Comparing the above acceleration expression with standard SHM equation a = – ω2x, we get
`ω^2 = (4k)/M`
⇒ `ω = sqrt((4K)/M)`
∴ Time period T = `(2pi)/ω = (2pi)/sqrt((4K)/M) = 2pi sqrt(M/(4k))`
APPEARS IN
RELATED QUESTIONS
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
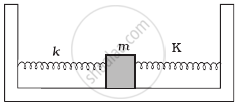
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
When will the motion of a simple pendulum be simple harmonic?
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
