Advertisements
Advertisements
Question
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Advertisements
Solution
Given the potential energy associated with the field
U(x) = U0 (1 – cos αx) [∵ For conservative force f, we can write f = `(-du)/(dx)`] ......(i)
Now, Force F = `- (dU(x))/(dx)` .....[We have assumed the field to be conservative]
F = `- d/(dx) (U_0 - U_0 cos ax) = - U_0 a sin ax`
F = `- U_0 a^2x` [∵ For small oscillations ax is small, sin ax ≈ ax] ......(ii)
⇒ F ∝ (– x)
As, U0, a being constant.
∴ Motion is S.H.M for small oscillations.
The standard equation for S.H.M F = `- mω^2x` ......(iii)
Comparing equations (ii) and (iii), we get
`mω^2 = U_0a^2`
`ω^2 = (U_0a^2)/m` or `ω = sqrt((U_0a^2)/m)`
∴ Time period T = `(2pi)/ω = 2pi sqrt(m/(U_0a^2))`
APPEARS IN
RELATED QUESTIONS
If the metal bob of a simple pendulum is replaced by a wooden bob of the same size, then its time period will.....................
- increase
- remain same
- decrease
- first increase and then decrease.
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
Define practical simple pendulum
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
When will the motion of a simple pendulum be simple harmonic?
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
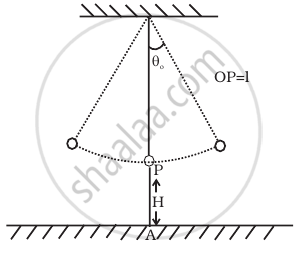
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
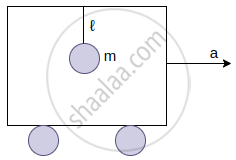
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is `x/2` times its original time period. Then the value of x is ______.
