Advertisements
Advertisements
Question
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
Solution
Consider the diagram of the spring block system. It is an S.H.M. with an amplitude of 5 cm about the mean position shown.
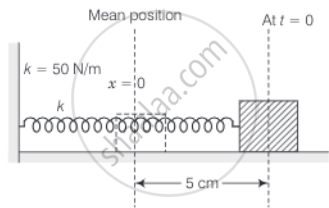
Given, the spring constant k = 50 N/m
m = mass attached = 2 kg
∴ Angular frequency `ω = sqrt(k/m)`
= `sqrt(50/2)`
= `sqrt(25)`
= 5 rad/s
Assuming the displacement function
`y(t) = Asin(ωt + phi)`
Where `phi` = initial phase
But given at t = 0, y(t) = + A
y(0) = + A = Asin(ω × 0 + `phi`)
or `sin phi` = 1 ⇒ `phi = pi/2`
∴ The desired equation is `y(t) = Asin(ωt + pi/2) = Acos ωt`
Putting A = 5 cm, ω = 5 rad/s
We get, y(t) = 5sin5t
Where t is in second and y is in centimetre.
APPEARS IN
RELATED QUESTIONS
A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
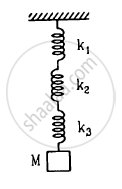
Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Displacement versus time curve for a particle executing S.H.M. is shown in figure. Identify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.

An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
