Advertisements
Advertisements
प्रश्न
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
उत्तर
Consider the diagram of the spring block system. It is an S.H.M. with an amplitude of 5 cm about the mean position shown.
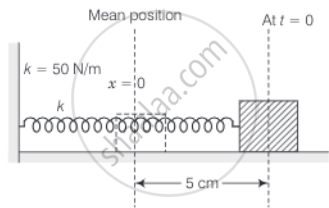
Given, the spring constant k = 50 N/m
m = mass attached = 2 kg
∴ Angular frequency `ω = sqrt(k/m)`
= `sqrt(50/2)`
= `sqrt(25)`
= 5 rad/s
Assuming the displacement function
`y(t) = Asin(ωt + phi)`
Where `phi` = initial phase
But given at t = 0, y(t) = + A
y(0) = + A = Asin(ω × 0 + `phi`)
or `sin phi` = 1 ⇒ `phi = pi/2`
∴ The desired equation is `y(t) = Asin(ωt + pi/2) = Acos ωt`
Putting A = 5 cm, ω = 5 rad/s
We get, y(t) = 5sin5t
Where t is in second and y is in centimetre.
APPEARS IN
संबंधित प्रश्न
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
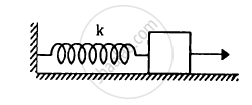
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find (a) the amplitude and the time period of the motion of the block, (b) the energy stored in the spring when the block passes through the equilibrium position and (c) the kinetic energy of the block at this position.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.

A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
What is the amplitude of oscillation?
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
