Advertisements
Advertisements
प्रश्न
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
उत्तर
It is given that:
Maximum speed of the particle, \[v_{Max}\]= `10 "cm"^(- 1)`
Maximum acceleration of the particle,
\[\Rightarrow \omega^2 = \frac{50}{A} . . . (2)\]
\[\text { From the equations (1) and (2), we get:} \]
\[\frac{100}{A^2} = \frac{50}{A}\]
\[ \Rightarrow A = 2 cm\]
\[ \therefore \omega = \sqrt{\frac{100}{A^2}} = 5 \sec^{- 1}\]
To determine the positions where the speed of the particle is 8 ms-1, we may use the following formula:
v2 = ω2 (A2 − y2)
where y is distance of particle from the mean position, and
v is velocity of the particle.
On substituting the given values in the above equation, we get:
64 = 25 (4 − y2)
\[\Rightarrow \frac{64}{25} = 4 - y^2\]
⇒ 4 − y2 = 2.56
⇒ y2 = 1.44
⇒ y = \[\sqrt{1 . 44}\]
⇒ y = ± 1.2 cm (from the mean position)
APPEARS IN
संबंधित प्रश्न
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
Consider a particle moving in simple harmonic motion according to the equation x = 2.0 cos (50 πt + tan−1 0.75) where x is in centimetre and t in second. The motion is started at t = 0. (a) When does the particle come to rest for the first time? (b) When does he acceleration have its maximum magnitude for the first time? (c) When does the particle come to rest for the second time ?
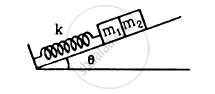
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
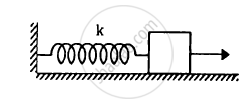
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find (a) the amplitude and the time period of the motion of the block, (b) the energy stored in the spring when the block passes through the equilibrium position and (c) the kinetic energy of the block at this position.
Repeat the previous exercise if the angle between each pair of springs is 120° initially.
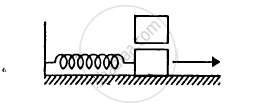
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
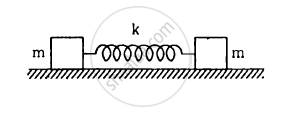
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.

A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
Discuss in detail the energy in simple harmonic motion.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Displacement versus time curve for a particle executing S.H.M. is shown in figure. Identify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.

An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
The total energy of a particle, executing simple harmonic motion is ______.
where x is the displacement from the mean position, hence total energy is independent of x.
