Advertisements
Advertisements
प्रश्न
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
Advertisements
उत्तर १
(a) Zero, Positive, Positive
(b) Zero, Negative, Negative
(c) Negative, Zero, Zero
(d) Negative, Negative, Negative
(e) Zero, Positive, Positive
(f) Negative, Negative, Negative
Explanation:
The given situation is shown in the following figure. Points A and B are the two end points, with AB = 10 cm. O is the midpoint of the path.
A particle is in linear simple harmonic motion between the end points
a) At the extreme point A, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is positive as it is directed along AO.
Force is also positive in this case as the particle is directed rightward.
b) At the extreme point B, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is negative as it is directed along B.
Force is also negative in this case as the particle is directed leftward.
c)
The particle is executing a simple harmonic motion. O is the mean position of the particle. Its velocity at the mean position O is the maximum. The value for velocity is negative as the particle is directed leftward. The acceleration and force of a particle executing SHM is zero at the mean position.
d)
The particle is moving toward point O from the end B. This direction of motion is opposite to the conventional positive direction, which is from A to B. Hence, the particle’s velocity and acceleration, and the force on it are all negative.
e)
The particle is moving toward point O from the end A. This direction of motion is from A to B, which is the conventional positive direction. Hence, the values for velocity, acceleration, and force are all positive.
f)
This case is similar to the one given in (d).
उत्तर २
In the fig. (given below), the points A and B, 10 cm apart, are the extreme positions of the particle in SHM, and the point O is the mean position. The direction from A to B is positive, as indicated.
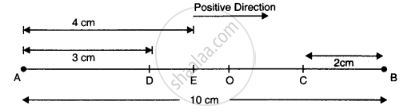
a) At the end A, i.e., extreme position, velocity is zero, acceleration and force are directed towards O and are positive.
(b) At the end B, i.e., second extreme position, velocity is zero whereas the acceleration and force are directed towards the point O and are negative.
(c) At the mid point O, while going towards A, velocity is negative and maximum. The acceleration and force both are zero.
(d) At 2 cm away from B, that is, at C and going towards A: v is negative; acceleration and F, being directed towards O, are also negative.
(e) At 3 cm away from A, that is, at D and going towards B: v is positive; acceleration and F, being directed towards O, are also positive.
(f) At a distance of 4 cm away from A and going towards A, velocity is directed along BA, therefore, it is positive. Since acceleration and force are directed towards OB, both of them are positive
संबंधित प्रश्न
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.
Discuss in detail the energy in simple harmonic motion.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Motion of an oscillating liquid column in a U-tube is ______.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
The total energy of a particle, executing simple harmonic motion is ______.
where x is the displacement from the mean position, hence total energy is independent of x.
