Advertisements
Advertisements
प्रश्न
Show that for a particle executing simple harmonic motion.
- the average value of kinetic energy is equal to the average value of potential energy.
- average potential energy = average kinetic energy = `1/2` (total energy)
Hint: average kinetic energy = <kinetic energy> = `1/"T" int_0^"T" ("Kinetic energy") "dt"` and
average potential energy = <potential energy> = `1/"T" int_0^"T" ("Potential energy") "dt"`
उत्तर
Suppose a particle of mass m executes SHM of period T.
The displacement of the particles at any instant t is given by y = A sin ωt
Velocity v = `"dy"/"dt" = ω"A" cos ω"t"`
Kinetic energy, EK = `1/2 "mv"^2 = 1/2"m"ω^2 "A"^2 cos^2 ω"t"`
Potential energy, EP = `1/2"m"ω^2"y"^2 = 1/2"m"ω^2 "A"^2 sin^2 ω"t"`
a. Average K.E. over a period of oscillation,
`"E"_("K"_"av") = 1/"T" int_0^"T" "E"_"K" "dt"`
= `1/"T" int_0^"T" 1/2 "m"ω^2 "A"^2 cos^2 ω"t" "dt"`
= `1/(2"T")"m"ω^2 "A"^2 int_0^"T" [(1 + cos 2 ω"t")/2] "dt"`
= `1/(4"T")"m"ω^2 "A"^2 ["t" + (sin 2 ω"t")/(2ω)]_0^"T"`
= `1/(4"T")"m"ω^2 "A"^2 "T"`
`"E"_("K"_"av") = 1 /4"m"ω^2 "A"^2`
b. Average P.E. over a period of oscillation
`"E"_("P"_"av") = 1/"T" int_0^"T" "E"_"P" "dt"`
= `1/"T" int_0^"T" 1/2 "m"ω^2 "A"^2 sin^2 ω"t" "dt"`
= `1/(2"T")"m"ω^2 "A"^2 int_0^"T" [(1 - cos 2 ω"t")/2] "dt"`
= `1/(4"T")"m"ω^2 "A"^2 ["t" - (sin 2 ω"t")/(2ω)]_0^"T"`
= `1/(4"T")"m"ω^2 "A"^2 "T"`
`"E"_("P"_"av") = 1 /4"m"ω^2 "A"^2`
APPEARS IN
संबंधित प्रश्न
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
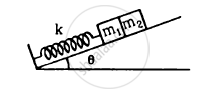
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
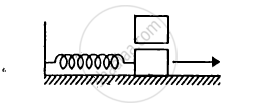
A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
Discuss in detail the energy in simple harmonic motion.
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Motion of an oscillating liquid column in a U-tube is ______.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
