Advertisements
Advertisements
प्रश्न
Discuss in detail the energy in simple harmonic motion.
Advertisements
उत्तर
Energy in simple harmonic motion:
(a) Expression for Potential Energy: For the simple harmonic motion, the force and the displacement are related by Hooke’s law
`vec"F" = -"k"vec("r")`
Since force is a vector quantity, in three dimensions it has three components.
Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case
F = − kx .....................(1)
The work done by the conservative force field is independent of the path. The potential energy U can be calculated from the following expression.
F = `-"dU"/"dx"` ..........(2)
Comparing (1) and (2), we get
`-"dU"/"dx" = -"kx"`
dU = kx dx
This work done by the force F during a small displacement dx stores as potential energy
U(x) = `int_0^"x" "kx′" "dx′" = 1/2["k"("x′")^2]_0^"x" = 1/2"kx"^2` ..........(3)
From equation `ω = sqrt("k"/"m")`, we can substitute the value of force constant k = mω2 in equation (3),
U(x) = `1/2"m"ω^2"x"^2` ...................(4)
where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation y = A sin ωt, we get
x = A sin ωt
U(t) = `1/2"m"ω^2"A"^2 sin^2ω"t"` ............(5)
This variation of U is shown in figure.
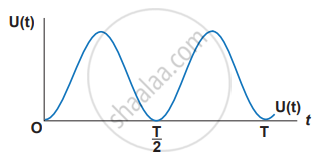
Variation of potential energy with time t
(b) Expression for Kinetic Energy:
Kinetic energy KE = `1/2"mv"_"x"^2 = 1/2"m" ("dx"/"dt")^2` ............(6)
Since the particle is executing simple harmonic motion, from equation y = A sin ωt
x = A sin ωt
Therefore, velocity is
vx = `"dx"/"dt"` = Aω cos ωt ...................(7)
= `"A"ω sqrt(1 - ("x"/"A")^2)`
vx = `ω sqrt("A"^2 - "x"^2)`
Hence, KE = `1/2"mv"_"x"^2 = 1/2"m"ω^2 ("A"^2 - "x"^2)` ........(9)
KE = `1/2"m"ω^2 "A"^2 cos^2 ω"t"` ..............(10)
This variation with time is shown in figure.
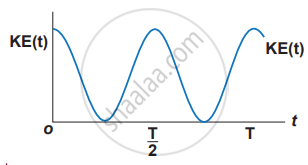
Variation of kinetic energy with time t
(c) Expression for Total Energy: Total energy is the sum of kinetic energy and potential energy
E = KE + U ..........…(11)
E = `1/2"m"ω^2 ("A"^2 - "x"^2) + 1/2 "m"ω^2 "x"^2`
Hence, cancelling x2 term,
E = `1/2"m"ω^2"A"^2` = constant ...............(12)
Alternatively, from equation (5) and equation (10), we get the total energy as
E = `1/2"m"ω^2"A"^2 sin^2 ω"t" + 1/2"m"ω^2"A"^2 cos^2 ω"t"`
= `1/2"m"ω^2"A"^2 (sin^2 ω"t" + cos^2 ω"t")`
From trigonometry identity, (sin2 ωt + cos2 ωt) = 1
E = `1/2"m"ω^2"A"^2` = constant
which gives the law of conservation of total energy. This is depicted in Figure
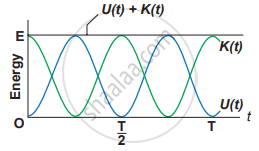
Both kinetic energy and potential energy vary but total energy is constant
Thus the amplitude of a simple harmonic oscillator can be expressed in terms of total energy.
A = `sqrt((2"E")/("m"ω^2)) = sqrt((2"E")/"k")` ..........(13)
APPEARS IN
संबंधित प्रश्न
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
In following figure k = 100 N/m M = 1 kg and F = 10 N.
- Find the compression of the spring in the equilibrium position.
- A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
- Find the time period of the resulting simple harmonic motion.
- Find the amplitude.
- Write the potential energy of the spring when the block is at the left extreme.
- Write the potential energy of the spring when the block is at the right extreme.
The answer of b, e and f are different. Explain why this does not violate the principle of conservation of energy.
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.
Show that for a particle executing simple harmonic motion.
- the average value of kinetic energy is equal to the average value of potential energy.
- average potential energy = average kinetic energy = `1/2` (total energy)
Hint: average kinetic energy = <kinetic energy> = `1/"T" int_0^"T" ("Kinetic energy") "dt"` and
average potential energy = <potential energy> = `1/"T" int_0^"T" ("Potential energy") "dt"`
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
