Advertisements
Advertisements
प्रश्न
Discuss in detail the energy in simple harmonic motion.
उत्तर
Energy in simple harmonic motion:
(a) Expression for Potential Energy: For the simple harmonic motion, the force and the displacement are related by Hooke’s law
`vec"F" = -"k"vec("r")`
Since force is a vector quantity, in three dimensions it has three components.
Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case
F = − kx .....................(1)
The work done by the conservative force field is independent of the path. The potential energy U can be calculated from the following expression.
F = `-"dU"/"dx"` ..........(2)
Comparing (1) and (2), we get
`-"dU"/"dx" = -"kx"`
dU = kx dx
This work done by the force F during a small displacement dx stores as potential energy
U(x) = `int_0^"x" "kx′" "dx′" = 1/2["k"("x′")^2]_0^"x" = 1/2"kx"^2` ..........(3)
From equation `ω = sqrt("k"/"m")`, we can substitute the value of force constant k = mω2 in equation (3),
U(x) = `1/2"m"ω^2"x"^2` ...................(4)
where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation y = A sin ωt, we get
x = A sin ωt
U(t) = `1/2"m"ω^2"A"^2 sin^2ω"t"` ............(5)
This variation of U is shown in figure.
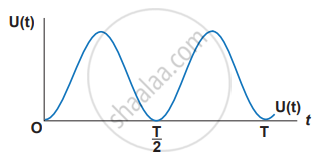
Variation of potential energy with time t
(b) Expression for Kinetic Energy:
Kinetic energy KE = `1/2"mv"_"x"^2 = 1/2"m" ("dx"/"dt")^2` ............(6)
Since the particle is executing simple harmonic motion, from equation y = A sin ωt
x = A sin ωt
Therefore, velocity is
vx = `"dx"/"dt"` = Aω cos ωt ...................(7)
= `"A"ω sqrt(1 - ("x"/"A")^2)`
vx = `ω sqrt("A"^2 - "x"^2)`
Hence, KE = `1/2"mv"_"x"^2 = 1/2"m"ω^2 ("A"^2 - "x"^2)` ........(9)
KE = `1/2"m"ω^2 "A"^2 cos^2 ω"t"` ..............(10)
This variation with time is shown in figure.
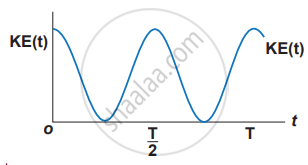
Variation of kinetic energy with time t
(c) Expression for Total Energy: Total energy is the sum of kinetic energy and potential energy
E = KE + U ..........…(11)
E = `1/2"m"ω^2 ("A"^2 - "x"^2) + 1/2 "m"ω^2 "x"^2`
Hence, cancelling x2 term,
E = `1/2"m"ω^2"A"^2` = constant ...............(12)
Alternatively, from equation (5) and equation (10), we get the total energy as
E = `1/2"m"ω^2"A"^2 sin^2 ω"t" + 1/2"m"ω^2"A"^2 cos^2 ω"t"`
= `1/2"m"ω^2"A"^2 (sin^2 ω"t" + cos^2 ω"t")`
From trigonometry identity, (sin2 ωt + cos2 ωt) = 1
E = `1/2"m"ω^2"A"^2` = constant
which gives the law of conservation of total energy. This is depicted in Figure
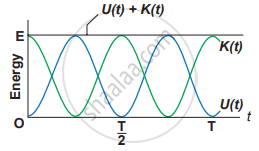
Both kinetic energy and potential energy vary but total energy is constant
Thus the amplitude of a simple harmonic oscillator can be expressed in terms of total energy.
A = `sqrt((2"E")/("m"ω^2)) = sqrt((2"E")/"k")` ..........(13)
APPEARS IN
संबंधित प्रश्न
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
Repeat the previous exercise if the angle between each pair of springs is 120° initially.
Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.

A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
What is the amplitude of oscillation?
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
