Advertisements
Advertisements
प्रश्न
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.
Advertisements
उत्तर
Let m is the mass of rectangular plate and x is the displacement of the rectangular plate.
During the oscillation, the centre of mass does not change.
Driving force \[\left( F \right)\] is given as,
F = mgsin θ
Comparing the above equation with F = ma, we get:
\[a = \frac{F}{m} = g\sin\theta\]
For small values of θ, sinθ can be taken as equal to θ.
Thus, the above equation reduces to:
\[a = g\theta = g\left( \frac{x}{L} \right) \left[ \text { Where g and L are constant .} \right]\]
It can be seen from the above equation that, a α x.
Hence, the motion is simple harmonic.
Time period of simple harmonic motion \[\left( T \right)\]is given by,
\[T = 2\pi\sqrt{\frac{\text { displacement }}{\text { Acceleration }}}\]
\[ = 2\pi\sqrt{\frac{x}{gx/L}} = 2\pi\sqrt{\frac{L}{g}}\]
APPEARS IN
संबंधित प्रश्न
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
Consider a particle moving in simple harmonic motion according to the equation x = 2.0 cos (50 πt + tan−1 0.75) where x is in centimetre and t in second. The motion is started at t = 0. (a) When does the particle come to rest for the first time? (b) When does he acceleration have its maximum magnitude for the first time? (c) When does the particle come to rest for the second time ?
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
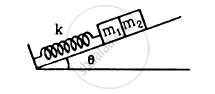
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
In following figure k = 100 N/m M = 1 kg and F = 10 N.
- Find the compression of the spring in the equilibrium position.
- A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
- Find the time period of the resulting simple harmonic motion.
- Find the amplitude.
- Write the potential energy of the spring when the block is at the left extreme.
- Write the potential energy of the spring when the block is at the right extreme.
The answer of b, e and f are different. Explain why this does not violate the principle of conservation of energy.
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
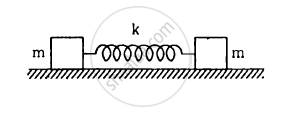
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
Discuss in detail the energy in simple harmonic motion.
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Motion of an oscillating liquid column in a U-tube is ______.
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
