Advertisements
Advertisements
प्रश्न
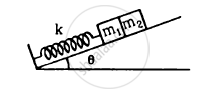
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
उत्तर
(a) As it can be seen from the figure,
Restoring force = kx
Component of total weight of the two bodies acting vertically downwards = (m1 + m2) g sin θ
At equilibrium,
kx = (m1 + m2) g sin θ
\[\Rightarrow x = \frac{\left( m_1 + m_2 \right) g \sin \theta}{k}\]
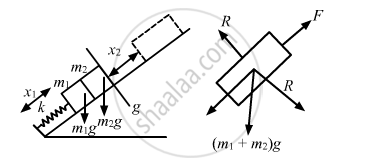
(b) It is given that:
Distance at which the spring is pushed,
\[x_1 = \frac{2}{k}\left( m_1 + m_2 \right)g \sin \theta\]
As the system is released, it executes S.H.M.
where \[\omega = \sqrt{\frac{k}{m_1 + m_2}}\]
When the blocks lose contact, P becomes zero. (P is the force exerted by mass m1 on mass m2)
\[\therefore m_2 g \sin \theta = m_2 x_2 \omega^2 = m_2 x_2 \times \frac{k}{m_1 + m_2}\] \[ \Rightarrow x_2 = \frac{\left( m_1 + m_2 \right) g \sin \theta}{k}\]
Therefore, the blocks lose contact with each other when the spring attains its natural length.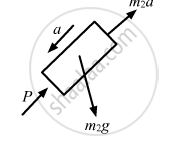
(c) Let v be the common speed attained by both the blocks.
\[\text { Total compression } = x_1 + x_2 \]
\[\frac{1}{2} \left( m_1 + m_2 \right) v^2 - 0 = \frac{1}{2}k \left( x_1 + x_2 \right)^2 - \left( m_1 + m_2 \right) g \sin \theta \left( x + x_1 \right) \]
\[ \Rightarrow \frac{1}{2}\left( m_1 + m_2 \right) v^2 = \frac{1}{2}k\left( \frac{3}{k} \right) \left( m_1 + m_2 \right) g \sin \theta - \left( m_1 + m_2 \right) g \sin \theta \left( x_1 + x_2 \right)\]
\[ \Rightarrow \frac{1}{2}\left( m_1 + m_2 \right) v^2 = \frac{1}{2} \left( m_1 + m_2 \right) g \sin \theta \times \left( \frac{3}{k} \right) \left( m_1 + m_2 \right) g sin \theta\]
\[ \Rightarrow v = \sqrt{\left\{ \frac{3}{k} \left( m_1 + m_2 \right) \right\}}g \sin \theta\]
APPEARS IN
संबंधित प्रश्न
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
Consider a particle moving in simple harmonic motion according to the equation x = 2.0 cos (50 πt + tan−1 0.75) where x is in centimetre and t in second. The motion is started at t = 0. (a) When does the particle come to rest for the first time? (b) When does he acceleration have its maximum magnitude for the first time? (c) When does the particle come to rest for the second time ?
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
Show that for a particle executing simple harmonic motion.
- the average value of kinetic energy is equal to the average value of potential energy.
- average potential energy = average kinetic energy = `1/2` (total energy)
Hint: average kinetic energy = <kinetic energy> = `1/"T" int_0^"T" ("Kinetic energy") "dt"` and
average potential energy = <potential energy> = `1/"T" int_0^"T" ("Potential energy") "dt"`
If a body is executing simple harmonic motion and its current displacements is `sqrt3/2` times the amplitude from its mean position, then the ratio between potential energy and kinetic energy is:
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
What is the amplitude of oscillation?
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
The total energy of a particle, executing simple harmonic motion is ______.
where x is the displacement from the mean position, hence total energy is independent of x.
