Advertisements
Advertisements
Question
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
Advertisements
Solution 1
(a) Zero, Positive, Positive
(b) Zero, Negative, Negative
(c) Negative, Zero, Zero
(d) Negative, Negative, Negative
(e) Zero, Positive, Positive
(f) Negative, Negative, Negative
Explanation:
The given situation is shown in the following figure. Points A and B are the two end points, with AB = 10 cm. O is the midpoint of the path.
A particle is in linear simple harmonic motion between the end points
a) At the extreme point A, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is positive as it is directed along AO.
Force is also positive in this case as the particle is directed rightward.
b) At the extreme point B, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is negative as it is directed along B.
Force is also negative in this case as the particle is directed leftward.
c)
The particle is executing a simple harmonic motion. O is the mean position of the particle. Its velocity at the mean position O is the maximum. The value for velocity is negative as the particle is directed leftward. The acceleration and force of a particle executing SHM is zero at the mean position.
d)
The particle is moving toward point O from the end B. This direction of motion is opposite to the conventional positive direction, which is from A to B. Hence, the particle’s velocity and acceleration, and the force on it are all negative.
e)
The particle is moving toward point O from the end A. This direction of motion is from A to B, which is the conventional positive direction. Hence, the values for velocity, acceleration, and force are all positive.
f)
This case is similar to the one given in (d).
Solution 2
In the fig. (given below), the points A and B, 10 cm apart, are the extreme positions of the particle in SHM, and the point O is the mean position. The direction from A to B is positive, as indicated.
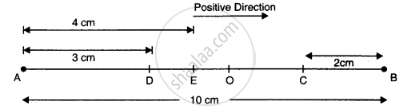
a) At the end A, i.e., extreme position, velocity is zero, acceleration and force are directed towards O and are positive.
(b) At the end B, i.e., second extreme position, velocity is zero whereas the acceleration and force are directed towards the point O and are negative.
(c) At the mid point O, while going towards A, velocity is negative and maximum. The acceleration and force both are zero.
(d) At 2 cm away from B, that is, at C and going towards A: v is negative; acceleration and F, being directed towards O, are also negative.
(e) At 3 cm away from A, that is, at D and going towards B: v is positive; acceleration and F, being directed towards O, are also positive.
(f) At a distance of 4 cm away from A and going towards A, velocity is directed along BA, therefore, it is positive. Since acceleration and force are directed towards OB, both of them are positive
RELATED QUESTIONS
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
If a body is executing simple harmonic motion and its current displacements is `sqrt3/2` times the amplitude from its mean position, then the ratio between potential energy and kinetic energy is:
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is performing S.H.M. Then its ______.
- average total energy per cycle is equal to its maximum kinetic energy.
- average kinetic energy per cycle is equal to half of its maximum kinetic energy.
- mean velocity over a complete cycle is equal to `2/π` times of its π maximum velocity.
- root mean square velocity is times of its maximum velocity `1/sqrt(2)`.
Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
What is the amplitude of oscillation?
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
