Advertisements
Advertisements
Question
A body is performing S.H.M. Then its ______.
- average total energy per cycle is equal to its maximum kinetic energy.
- average kinetic energy per cycle is equal to half of its maximum kinetic energy.
- mean velocity over a complete cycle is equal to `2/π` times of its π maximum velocity.
- root mean square velocity is times of its maximum velocity `1/sqrt(2)`.
Solution
a, b and d
Explanation:
In the case of S.H.M, the average total energy per cycle
= Maximum kinetic energy (K0)
= Maximum potential energy (U0)
Average KE per cycle = `(0 + K_0)/2 = K_0/2`
Let us write the equation for the SHM x = a sin ωt.
Clearly, it is a periodic motion as it involves a sine function.
Let us find velocity of the particle, `v = (dx)/(dt) = d/(dt) (a sin ωt) = aω cos ωt`
Mean velocity over a complete cycle,
`v_"mean" = (int_0^(2pi) ωa cos θd θ)/(2pi)`
= `(ωa[sin θ]_0^(2pi))/(2pi)`
= 0
So, `v_"mean" ≠ 2/pi v_"max"`
Root mean square speed,
`v_(rms) = sqrt((v_"min"^2 + v_"max"^2)/2`
= `sqrt((0 + v_"max"^2)/2`
`v_(rms) = 1/sqrt(2) v_"max"`
APPEARS IN
RELATED QUESTIONS
A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
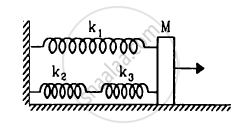
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.

A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
The total energy of a particle, executing simple harmonic motion is ______.
where x is the displacement from the mean position, hence total energy is independent of x.
