Advertisements
Advertisements
Question
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
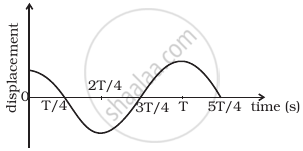
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
Solution
a, b and c
Explanation:
Consider the diagram
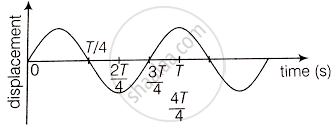
From the given diagram; it is clear that
- At `t = (3T)/4`, the displacement of the particle is zero. Hence. the particle executing SHM will be at the mean position ie., x = 0. So, acceleration is zero and force is also zero.
- At t = `(4T)/4`, displacement is maximum i.e., extreme position, so acceleration is maximum.
- At t = `T/4`, corresponds to the mean position. so velocity will be maximum at this position.
- At t = `(2T)/4 = T/2`, corresponds to extreme position, so KE = 0 and PE = maximum.
APPEARS IN
RELATED QUESTIONS
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
A body of mass 1 kg is mafe to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequency, (b) Frequency of vibrations.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
A particle performs simple harmonic motion with a period of 2 seconds. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is `1/a` s. The value of 'a' to the nearest integer is ______.
