Advertisements
Advertisements
Question
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
Solution
The ball moves to and fro about the lowermost point of the bowl when released. Also, the ball comes back to its initial position in the same period of time, again and again. Hence, its motion is periodic as well as simple harmonic.
APPEARS IN
RELATED QUESTIONS
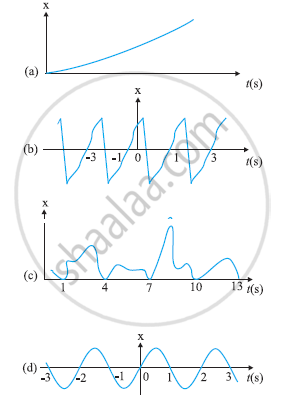
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.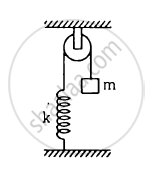
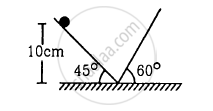
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
A simple pendulum is inside a spacecraft. What will be its periodic time?
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
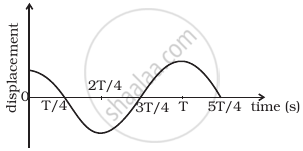
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
What are the two basic characteristics of a simple harmonic motion?
