Advertisements
Advertisements
Question
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
Options
k1/k2
\[\sqrt{k_1 / k_2}\]
k2/k1
\[\sqrt{k_2 / k_1}\]
Solution
\[\sqrt{\frac{k_2}{k_1}}\]
Maximum velocity, v = Aω
where A is amplitude and ω is the angular frequency.
Further, ω =\[\sqrt{\frac{k}{m}}\]
Let A and B be the amplitudes of particles A and B respectively. As the maximum velocity of particles are equal,
\[i . e . v_A = v_B \]
\[\text { or }, \]
\[ A \omega_A = B \omega_B \]
\[ \Rightarrow A\sqrt{\frac{k_1}{m_A}} = B\sqrt{\frac{k_2}{m_B}}\]
\[ \Rightarrow A\sqrt{\frac{k_1}{m}} = B\sqrt{\frac{k_2}{m}} ( m_A = m_B = m)\]
\[ \Rightarrow \frac{A}{B} = \sqrt{\frac{k_2}{k_1}}\]
APPEARS IN
RELATED QUESTIONS
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
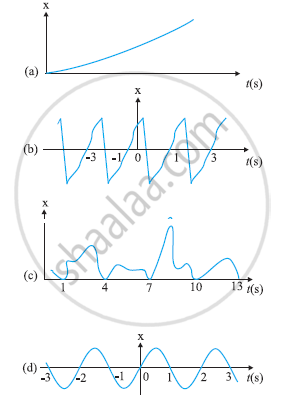
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A particle moves in a circular path with a uniform speed. Its motion is
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
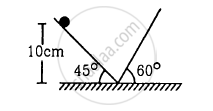
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
