Advertisements
Advertisements
प्रश्न
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
पर्याय
k1/k2
\[\sqrt{k_1 / k_2}\]
k2/k1
\[\sqrt{k_2 / k_1}\]
उत्तर
\[\sqrt{\frac{k_2}{k_1}}\]
Maximum velocity, v = Aω
where A is amplitude and ω is the angular frequency.
Further, ω =\[\sqrt{\frac{k}{m}}\]
Let A and B be the amplitudes of particles A and B respectively. As the maximum velocity of particles are equal,
\[i . e . v_A = v_B \]
\[\text { or }, \]
\[ A \omega_A = B \omega_B \]
\[ \Rightarrow A\sqrt{\frac{k_1}{m_A}} = B\sqrt{\frac{k_2}{m_B}}\]
\[ \Rightarrow A\sqrt{\frac{k_1}{m}} = B\sqrt{\frac{k_2}{m}} ( m_A = m_B = m)\]
\[ \Rightarrow \frac{A}{B} = \sqrt{\frac{k_2}{k_1}}\]
APPEARS IN
संबंधित प्रश्न
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
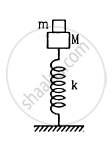
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.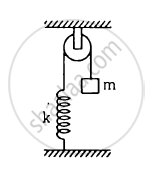
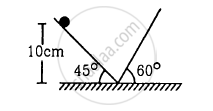
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

A body of mass 1 kg is mafe to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequency, (b) Frequency of vibrations.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
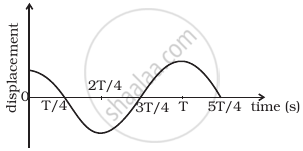
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
What are the two basic characteristics of a simple harmonic motion?
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
