Advertisements
Advertisements
प्रश्न
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

उत्तर
Given,
Length of the long, light suspension wire, l = 3 cm = 0.03 m
Acceleration due to gravity, `g = 9.8 "ms"^(- 2)`
(a)Time Period \[\left( T \right)\] is given by ,
\[T = 2\pi\sqrt{\left( \frac{l}{g} \right)}\]
\[ = 2\pi\sqrt{\left( \frac{0 . 03}{9 . 8} \right)}\]
\[ = 0 . 34 \text { second}\]
(b) Velocity of merry-go-round, v = 4 `"ms"^(- 1)`
Radius of circle, r = 2 m
As the lady sits on the merry-go-round, her earring experiences centripetal acceleration.
Centripetal acceleration (a) is given by,
\[a = \frac{v^2}{r} = \frac{4^2}{2} = 8 m/ s^2\]
Resultant acceleration (A) is given by ,
\[A = \sqrt{\left( g^2 + a^2 \right)}\]
\[ = \sqrt{\left( 96 . 04 + 64 \right)}\]
\[ = 12 . 65 m/ s^2\]
Time Period,
\[T = 2\pi\sqrt{\left( \frac{l}{A} \right)}\]
\[= 2\pi\sqrt{\left( \frac{0 . 03}{12 . 65} \right)}\]
\[ = 0 . 30 \text { second }\]
APPEARS IN
संबंधित प्रश्न
Which of the following example represent periodic motion?
An arrow released from a bow.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
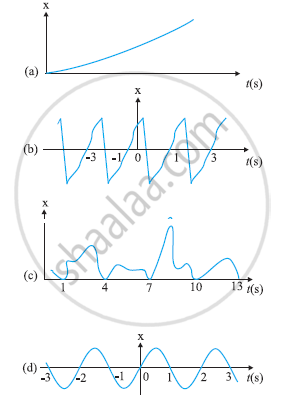
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
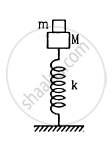
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
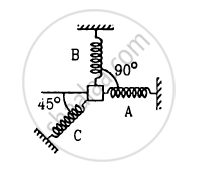
A particle of mass m is attatched to three springs A, B and C of equal force constants kas shown in figure . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
A simple pendulum is inside a spacecraft. What will be its periodic time?
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
