Advertisements
Advertisements
प्रश्न
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
उत्तर
It is given that a car is moving with speed v on a circular horizontal road of radius r.
(a) Let T be the tension in the string.
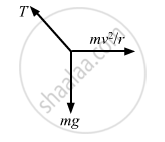
According to the free body diagram, the value of T is given as,
\[T = \sqrt{\left( mg \right)^2 + \left( \frac{m v^2}{r} \right)^2}\]
\[= m\sqrt{g^2 + \frac{v^4}{r^2}} = ma,\]
where acceleration, a \[= \sqrt{g^2 + \frac{v^4}{r^2}}\]
The time period \[\left( T \right)\] is given by ,
\[T = 2\pi\sqrt{\frac{l}{g}}\]
\[\text { On substituting the respective values, we have: } \]
\[T = 2\pi\sqrt{\frac{l}{\left( g^2 + \frac{v^4}{r^2} \right)^{1/2}}}\]
APPEARS IN
संबंधित प्रश्न
Define phase of S.H.M.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
It is proposed to move a particle in simple harmonic motion on a rough horizontal surface by applying an external force along the line of motion. Sketch the graph of the applied force against the position of the particle. Note that the applied force has two values for a given position depending on whether the particle is moving in positive or negative direction.
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The displacement of a particle in simple harmonic motion in one time period is
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
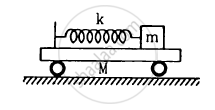
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
Define the time period of simple harmonic motion.
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

