Advertisements
Advertisements
प्रश्न
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
Advertisements
उत्तर
It is given that a car is moving with speed v on a circular horizontal road of radius r.
(a) Let T be the tension in the string.
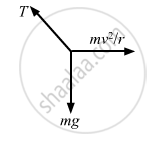
According to the free body diagram, the value of T is given as,
\[T = \sqrt{\left( mg \right)^2 + \left( \frac{m v^2}{r} \right)^2}\]
\[= m\sqrt{g^2 + \frac{v^4}{r^2}} = ma,\]
where acceleration, a \[= \sqrt{g^2 + \frac{v^4}{r^2}}\]
The time period \[\left( T \right)\] is given by ,
\[T = 2\pi\sqrt{\frac{l}{g}}\]
\[\text { On substituting the respective values, we have: } \]
\[T = 2\pi\sqrt{\frac{l}{\left( g^2 + \frac{v^4}{r^2} \right)^{1/2}}}\]
APPEARS IN
संबंधित प्रश्न
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
Can a pendulum clock be used in an earth-satellite?
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The distance moved by a particle in simple harmonic motion in one time period is
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
For a particle executing simple harmonic motion, the acceleration is proportional to
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
Define the time period of simple harmonic motion.
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
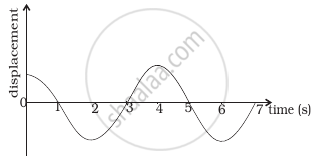
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
