Question

A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.

Answer 1

It is given that:
Length of the simple pendulum, l = 1  feet
Time period of simple pendulum, T = \[\frac{\pi}{3}  s\] Acceleration due to gravity, g = 32 ft/s²

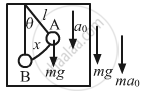
<sup>Let a be the acceleration of the elevator while moving upwards.
Driving force \[\left( f \right)\] is given by,
f = m(g + a)sinθ 

Comparing the above equation with the expression, f = ma, we get:
Acceleration, a  =  (g + a)sinθ = (g +a)θ              (For small angle θ, sin θ → θ)</sup>

^{\[= \frac{\left( g + a \right)x}{l} =  \omega^2 x\] (From the diagram \[\theta = \frac{x}{l}\])}

^{\[\Rightarrow \omega =   \sqrt{\frac{\left( g + a \right)}{l}}\]}

^{Time Period \[\left( T \right)\] is given as,}

^{\[T = 2\pi\sqrt{\frac{l}{g + a}}\]}

^{On substituting the respective values in the above formula, we get:}

\[\frac{\pi}{3} = 2\pi\sqrt{\frac{1}{32 + a}}\] 

\[\frac{1}{9} = 4\left( \frac{1}{32 + a} \right)\] 

\[ \Rightarrow 32 + a = 36\] 

\[ \Rightarrow a = 36 - 32 = 4  ft/ s^2\]