Advertisements
Advertisements
प्रश्न
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
उत्तर
Let x = A sin ω is the displacement function of SHM.
Velocity, `v = (dx)/(dt) = Aω cosωt`
`v_max = Aω |cos ωt|_"max"`
= `Aω xx 1`
= `ωA` [∵ |cos ωt|max = 1] ......(i)
Acceleration, `a = (dv)/(dt) = - ωA * ωsinωt`
= `- ω^2A sinωt`
`|a_max| = |(- ω^2A)(+1)|` ......[∵ (sin ωt)max = 1]
`|a_max| = ω^2A` .......(ii)
From equations (i) and (ii), we get
`v_max/a_max = (ωA)/(ω^2A) = 1/ω`
⇒ `a_max/v_max = ω`
APPEARS IN
संबंधित प्रश्न
Define phase of S.H.M.
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A particle moves in a circular path with a continuously increasing speed. Its motion is
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
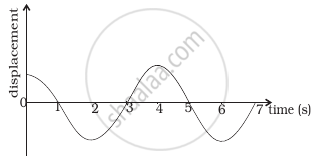
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
