Advertisements
Advertisements
प्रश्न
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
उत्तर
(c) on a straight line
(d) periodic
If the particle were dropped from the surface of the earth, the motion of the particle would be SHM. But when it is dropped from a height h, the motion of the particle is not SHM because there is no horizontal velocity imparted. In that case, the motion of the particle would be periodic and in a straight line.
APPEARS IN
संबंधित प्रश्न
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The distance moved by a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
Which of the following quantities are always positive in a simple harmonic motion?
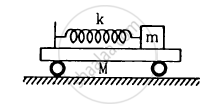
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
What is an epoch?
The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
