Advertisements
Advertisements
प्रश्न
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
उत्तर
Given are the equations of motion of a particle:
x1 = 2.0sin100 \[\pi\]t
\[x_2 = 2 . 0\sin\left( 120\pi t + \frac{\pi}{3} \right)\]
The Resultant displacement \[\left( x \right)\] will be
x = x1 + x2
\[= 2\left[ \sin\left( 100\pi t \right) + \sin\left( 120\pi t + \frac{\pi}{3} \right) \right]\]
(a) At t = 0.0125 s
\[x = 2\left[ \sin\left( 100\pi \times 0 . 0125 \right) + \sin\left( 120\pi \times 0 . 0125 + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \sin \left( \frac{5\pi}{4} \right) + \sin \left( \frac{3\pi}{2} + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \left( - 0 . 707 \right) + \left( - 0 . 5 \right) \right]\]
\[ = 2 \times \left( - 1 . 207 \right) = - 2 . 41 cm\]
(b) At t = 0.025 s
\[x = 2\left[ \sin\left( 100 \pi \times 0 . 025 \right) + \sin\left( 120\pi \times 0 . 025 + \frac{\pi}{3} \right) \right]\] \[ = 2\left[ \sin\left( \frac{10\pi}{4} \right) + \sin\left( 3\pi + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ 1 + \left( - 0 . 866 \right) \right]\]
\[ = 2 \times \left( 0 . 134 \right) = 0 . 27 \text { cm }\]
APPEARS IN
संबंधित प्रश्न
State the differential equation of linear simple harmonic motion.
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
The displacement of a particle in simple harmonic motion in one time period is
A particle moves in a circular path with a continuously increasing speed. Its motion is
For a particle executing simple harmonic motion, the acceleration is proportional to
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
(a) the measured times are same
(b) the measured speeds are same
(c) the actual times in the fall are equal
(d) the actual speeds are equal
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
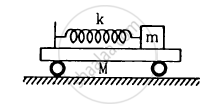
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
